Дві прямі, що зіштовхуються під гострим кутом дев’яносто градусів, створюють перпендикуляр – фундаментальний елемент геометрії, який тримає на собі стіни будинків, траєкторії куль і навіть віртуальні світи комп’ютерних ігор. Цей кут, такий чистий і впевнений, нагадує вертикальний схил будівельника, що перевіряє стійкість конструкції. Уявіть горизонтальну лінію дороги, а зверху – стовп ліхтаря, що стирчить рівно вгору: ось класичний перпендикуляр у дії.
У евклідовому просторі перпендикулярність визначається як відношення між об’єктами, де кут перетину дорівнює рівно 90 градусам. Це стосується не тільки прямих, а й векторів чи площин. Перпендикуляр – це не просто абстракція, а інструмент, що робить світ передбачуваним. Без нього не було б прямокутних координатних систем, на яких базується вся сучасна математика.
Перпендикулярні прямі на площині: від визначення до властивостей
На площині дві прямі називаються перпендикулярними, якщо вони перетинаються, утворюючи чотири рівні прямі кути по 90 градусів кожен. Символ ⊥ позначає це відношення: наприклад, a ⊥ b. Відрізки чи промені перпендикулярні, якщо лежать на таких прямих. Перпендикуляром з точки A до прямої l є відрізок від A до точки перетину H – основи перпендикуляра, а його довжина дорівнює відстані від точки до прямої.
Властивостей у перпендикулярів вистачає, щоб заповнити цілу главу підручника. Дві прямі, перпендикулярні до третьої, паралельні між собою – це базова теорема, яка допомагає будувати паралелі за допомогою косинця й лінійки. Через будь-яку точку площини до заданої прямої можна провести рівно одну перпендикулярну пряму. А якщо точки збігаються з прямою, то перпендикулярів безліч, утворюючи площину, перпендикулярну до даної.
Ознаки перпендикулярності прості, але хитрі. Якщо кути нахилу прямих α₁ і α₂ задовольняють tg α₂ = -1/tg α₁, то вони перпендикулярні. У координатах рівняння y = m₁x + b₁ і y = m₂x + b₂ дає m₁ · m₂ = -1. Ось приклад: пряма з нахилом 45° (m=1) перпендикулярна до m=-1, тобто нахилу -45°.
- Побудова перпендикуляра циркулем: від точки A накрестіть дугу, що перетинає пряму в B і C; з центрів B і C через A намалюйте дуги, що сходяться в D; лінійка AD – перпендикуляр.
- Серединний перпендикуляр відрізка AB: дуги з A і B перетинаються в двох точках, лінія між ними ділить AB навпіл і стоїть під 90°.
- У трикутнику: висота – перпендикуляр від вершини до протилежної сторони.
Ці методи не просто теорія – вони рятують на іспитах і в кресленнях. А тепер перейдімо до тривимірного світу, де перпендикуляри набувають нової сили.
Перпендикуляр у просторі: площини, прямі та похилі
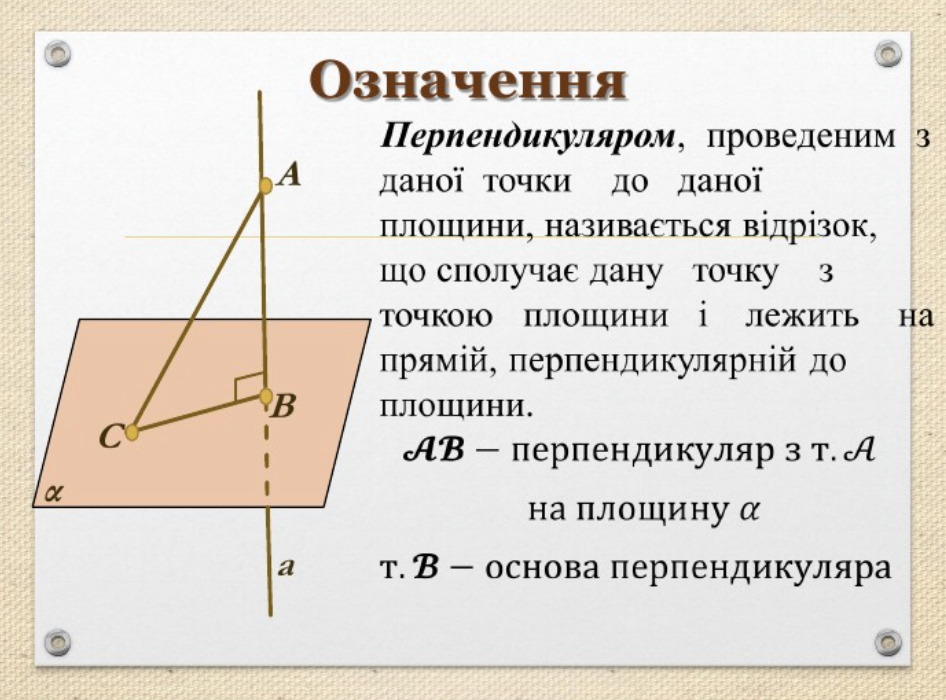
У тривимірному евклідовому просторі все ускладнюється, але правила лишаються логічними. Пряма перпендикулярна площині, якщо стоїть під 90° до кожної прямої в площині, що проходить через точку перетину. Основа – точка H на площині. Похила – будь-яка інша пряма з тієї ж точки до площини, а проекція – відрізок від H паралельно похилій.
Теорема про три перпендикуляри звучить як магія: якщо на площині через основу похилої провести перпендикуляр до її проекції, то він перпендикулярний і похилій. Дві площини перпендикулярні, якщо двогранний кут між ними 90°. Дві прямі в просторі перпендикулярні, якщо паралельні двом перпендикулярним прямим в одній площині.
| Тип взаємного розміщення | Визначення | Приклад | Символ |
|---|---|---|---|
| Перпендикулярні | Перетин під 90° | Стіна й підлога | ⊥ |
| Паралельні | Не перетинаються, рівні кути з третьою | Рейки залізниці | ∥ |
| Нахилені | Перетинаються під ≠90° | Дорога й річка | – |
| Криві | Не перетинаються в просторі | Дві гілки дерева | – |
Таблиця базується на даних з uk.wikipedia.org. Такі порівняння полегшують розуміння: перпендикуляр – найкоротший шлях, завжди мінімальний.
Векторна сутність перпендикуляра: скалярний добуток нуль
У векторній алгебрі перпендикулярність – коли скалярний добуток двох ненульових векторів дорівнює нулю: \(\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos 90^\circ = 0\). Це працює для прямих напрямків векторів. У координатах (a1, a2, a3) і (b1, b2, b3): a1 b1 + a2 b2 + a3 b3 = 0.
Наприклад, вектори (1,0) і (0,1) – осі xOy, їх добуток 0. У 3D: нормаль до площини ax+by+cz=d має вектор (a,b,c), перпендикулярний площині. Цей підхід революціонізував математику, бо перейшов від геометрії до алгебри.
У аналітичній геометрії перпендикулярні вектори ортогональні, основа для ортонормованих баз – як у системах координат.
Історія терміну: від Стародавньої Греції до сучасного символу
Поняття прямих кутів з’явилося в “Началах” Евкліда близько 300 р. до н.е., де V постулат торкався паралелей, але перпендикуляри були основою. Термін “перпендикуляр” походить від латинського “perpendiculum” – свинцевого схилу для перевірки вертикалі в будівництві. Римляни використовували його практично.
Символ ⊥ винайшов П’єр Ерігон у 1634 році в трактаті про конічні перетини. До того позначали літерами чи словами. Цей знак увійшов у стандарт, як і багато винаходів того часу.
Перпендикуляр у реальному світі: від фізики до цифрових технологій
У фізиці та інженерії
У фізиці перпендикуляр – нормаль до поверхні, напрямок реакції опори чи магнітного поля. Сила тяжіння діє перпендикулярно горизонту. У механіці момент сили максимальний, коли плече перпендикулярне силі. Інженери в мостах чи хмарочосах розраховують на перпендикулярні опори для стійкості – подивіться на Ейфелеву вежу, де діагоналі компенсують навантаження.
У комп’ютерній графіці та програмуванні
У 3D-графіці нормалі (перпендикуляри до поверхонь) визначають освітлення: кут падіння променя на нормаль дає інтенсивність світла. У OpenGL чи Unity векторні перпендикуляри будують координатні системи об’єктів. GPS розраховує відстані перпендикулярами до поверхні Землі. Навіть у машинному навчанні ортогональні базиси прискорюють обчислення.
Цікаві факти про перпендикуляр
- У Піфагоровій теоремі катети перпендикулярні, гіпотенуза – діагональ прямокутника.
- Найкоротший шлях від точки до прямої – перпендикуляр, принцип Ферма в оптиці.
- У кристалографії перпендикулярні осі визначають кубічні ґратки алмазів.
- Символ ⊥ нагадує схил – інструмент, що “зависав” перпендикулярно землі.
- У неевклідовій геометрії перпендикулярів може бути безліч або жодного до паралелі.
Типові помилки школярів: плутати з паралельними (вони не перетинаються) чи вважати, що в просторі всі перпендикуляри паралельні – ні, вони сходяться. Порада: малюйте моделі з олівців, щоб відчути простір.
Перпендикуляр пронизує все: від шкільних задач до космічних польотів. Спробуйте побудувати один удома – і побачите, як світ вирівнюється.














Залишити відповідь