Десятковий дріб ховається в кожній копійці гривні, в міліметрах тканини чи відсотках знижки на улюблений гаджет. Це число з комою, де права частина виражає частку від одиниці через степені десятки – 10, 100 чи тисячу. Наприклад, 3,14 не просто символ, а три цілих одиниці плюс чотирнадцять сотих. Такий запис перетворює абстрактні частки на зручний інструмент для щоденних розрахунків.
У математиці десятковий дріб дорівнює звичайному дробу з знаменником 10n, де n – кількість знаків після коми. 0,75 це 75/100, або спрощено 3/4. Ця форма народилася з потреби швидко рахувати в торгівлі та інженерії, роблячи дроби видимими без рисків знаменників. Розуміння його дозволяє уникати плутанини в фінансах чи наукових даних.
Крапка чи кома розділяє цілу частину від дробової, залежно від країни. В Україні кома править бал, перетворюючи 0,25 на чверть яблука. Тепер зануримося глибше, розбираючи, як цей скромний символ еволюціонував і чому іноді б’є по нервах програмістів.
Історія народження десяткового дробу
Уявіть Європу XVI століття: купці мучаться з римськими цифрами, а інженери рахують мости на пальцях. Нідерландський геній Сімон Стевін у 1585 році видає трактат “De Thiende” – сім сторінок, що перевернули математику. Він запропонував записувати частки десятками, як 0,5 для половини, замість громіздких 1/2. Стевін демонстрував, як це спрощує пропорції в торгівлі та фортифікаціях.
Хоча перші натяки з’явилися раніше – перський математик Джамшид аль-Каші у 1427 році використав десяткові для тригонометрії. Але саме Стевін зробив їх масовими в Європі, вплинувши на метричну систему. Сьогодні, за даними uk.wikipedia.org, його ідея лежить в основі глобальних стандартів обчислень.
Ця еволюція не зупинилася: у 2026 році десяткові дроби правлять у цифровому світі, від блокчейну до AI-моделей, де точність до шістнадцятого знака вирішує долю транзакцій.
Види десяткових дробів: від простих до загадкових
Десяткові дроби поділяються на скінченні та періодичні, ніби спокійні озера й бурхливі річки. Скінченні закінчуються після кількох знаків – 0,8 це 4/5, де знаменник 10 чи 100. Вони виникають, коли звичайний дріб має знаменник, що розкладається на 2 і 5.
Періодичні – це нескінченні повторювачі. Чистий періодичний, як 0,(3) для 1/3, де “3” циклічно танцює. Змішаний має неперіодичну частину перед циклом: 1,2(34) дорівнює 1 + 2/10 + 34/990. Ірраціональні, на кшталт π = 3,14159…, не повторюються взагалі, але апроксимуються десятковими.
Щоб розрізнити: поділіть чисельник на знаменник звичайного дробу. Якщо цикл починається одразу – чистий періодичний. Перед циклом цифри? Змішаний. За даними математичних посібників, 90% раціональних дробів стають періодичними, додаючи шар загадковості повсякденним розрахункам.
Таблиця розрядів десяткового дробу
Розряди – ключ до читання. Ось як цифри після коми відповідають часткам:
| Розряд | Десяткові | Назва | Приклад |
|---|---|---|---|
| 1-й | 0,1 | Десяті | 0,7 = 7/10 |
| 2-й | 0,01 | Соті | 0,05 = 5/100 |
| 3-й | 0,001 | Тисячі | 0,008 = 8/1000 |
| 4-й | 0,0001 | Десятитисячні | 0,0002 = 2/10000 |
Джерела даних: стандартні шкільні програми та uk.wikipedia.org. Ця таблиця спрощує порівняння: чим далі розряд, тим менша вага.
Читання, запис і порівняння десяткових дробів
Записуйте комою: 2,35 – дві цілих, три десятки, п’ять сотих. Читання йде зліва направо, акцентуючи коми. Порівнювати просто: вирівняйте коми, порівняйте по розрядах, ніби змагаються спортсмени на доріжках.
Наприклад, 0,99 > 0,9, бо другі розряди: 9 > нічого (нуль). Або 1,234 і 1,24 – допишіть нулі: 1,240, тепер 4 < 0? Ні, 234 > 240? Помилка в голові, але правило нулів рятує.
У житті це рятує від переплат: 12,99 грн дешевше за 13 грн? Так, бо 0,99 менше 1.
Арифметичні операції: додавання, віднімання, множення, ділення
Додавання та віднімання – як з цілими, але з вирівнюванням ком. Зрівняйте знаки після коми нулями: 2,3 + 1,24 = 2,30 + 1,24 = 3,54. Легко, ніби зшиваєте тканину рівними стібками.
Множення десяткових дробів
Множте як цілі, кома в добутку на суму знаків множників. 1,2 × 0,3: 12 × 3 = 36, два знаки – 0,36. Швидко, але стежте за нулями.
Ділення десяткових дробів
Перетворіть дільник на ціле, множачи на 10k, те саме з діленою. 4,5 ÷ 0,9: ×10 = 45 ÷ 9 = 5. Результат – п’ять одиниць, точний як годинник.
Ці операції – основа для складніших задач, від бюджетів до фізичних формул.
Перетворення між десятковими та звичайними дробами
Десятковий у звичайний: напишіть чисельник після коми, знаменник – 10n. 0,625 = 625/1000 = 5/8. Спростіть, і вуаля!
Зворотне: ділите чисельник на знаменник. 3/8 = 0,375 – скінченний. 1/3 = 0,(3) – періодичний. Якщо знаменник має тільки 2 і 5 – скінченний, інакше цикл.
- Приклад 1: 2/5 = 0,4 (скінченний).
- Приклад 2: 1/6 = 0,1(6) (змішаний).
- Приклад 3: 1/7 = 0,(142857) (чистий, період 6 цифр).
Після перетворення перевіряйте: помножте назад. Це гарантує точність у наукових обчисленнях.
Округлення: мистецтво наближення
Округлення робить числа керованими. До першого знака: 3,1416 ≈ 3,1 (6>5, округлили вгору). Правила: 5 і більше – +1, менше – 0.
У фінансах України округляють до двох знаків: 123,456 ≈ 123,46 грн. Банки слідують НБУ стандартам, уникаючи копійкових дрібниць.
Десяткові дроби в реальному житті: від кухні до космосу
На кухні: рецепт на 2,5 кг борошна ділите на 5 – 0,5 кг порція. У магазинах: 15% знижки з 999 грн – мінус 149,85 грн, лишається 849,15.
У спорті: спринтер пробіг 100 м за 9,58 с – рекорд з мілісекундами. Фізика: швидкість світла 299 792 458 м/с апроксимують 3×108.
Програмування: floating point – десяткові, але з пастками. 0,1 + 0,2 = 0,30000000000000004 через бінарне представлення. У 2026 році Python Decimal модуль рятує фінтех від втрат мільйонів.
Типові помилки при роботі з десятковими дробами
Перша пастка: забуваємо вирівнювати коми. Додаєте 1,2 + 0,34 як 1,2 + 0,3 = 1,5, але правильно 1,20 + 0,34 = 1,54. Результат хибний на 0,04 – як переплата в касі.
Друга: при множенні кома не на місці. 0,2 × 0,3: 2×3=6, один знак? Ні, два – 0,06. Початківці пишуть 0,6, завищуючи вдвічі.
Третя: ділення без перенесення коми. 12,5 ÷ 2,5: думаєте 5, але правильно ×10/×10 = 125÷25=5. Або ігнор нулів у дільнику – нульовий результат!
Четверта: округлення без правила. 1,24 до одного знака – не 1,2, а 1,2 (4<5), але 1,25 = 1,3. У фінансах це копійки, у статистиці – тисячі.
П’ята: плутанина з періодичними. 1/3 пишуть 0,333, забуваючи дужки (3). При перетворенні – помилка в знаменнику.
Уникайте, перевіряючи калькулятором чи перетворюючи в звичайні. Практика – ключ: розв’яжіть 10 прикладів щодня.
Ці помилки трапляються в 30% шкільних завдань, але з практикою зникають, роблячи вас майстром цифр.
Поглиблені аспекти: періодичні дроби та ірраціонали
Період 1/7 – 142857, що повторюється: 0,(142857). Цікаво, 142857 × 2 = 285714 – цикл зсувається! Такі властивості полегшують множення.
Ірраціонали як √2 = 1,414213… апроксимують для інженерії. У 2026 році суперкомп’ютери рахують π до трильйонів знаків, але для нас вистачить десятка.
Десятковий дріб – не просто знак, а місток до точного світу, де кожна цифра має вагу. Спробуйте розрахувати свій бюджет з ними – і відчуєте силу.
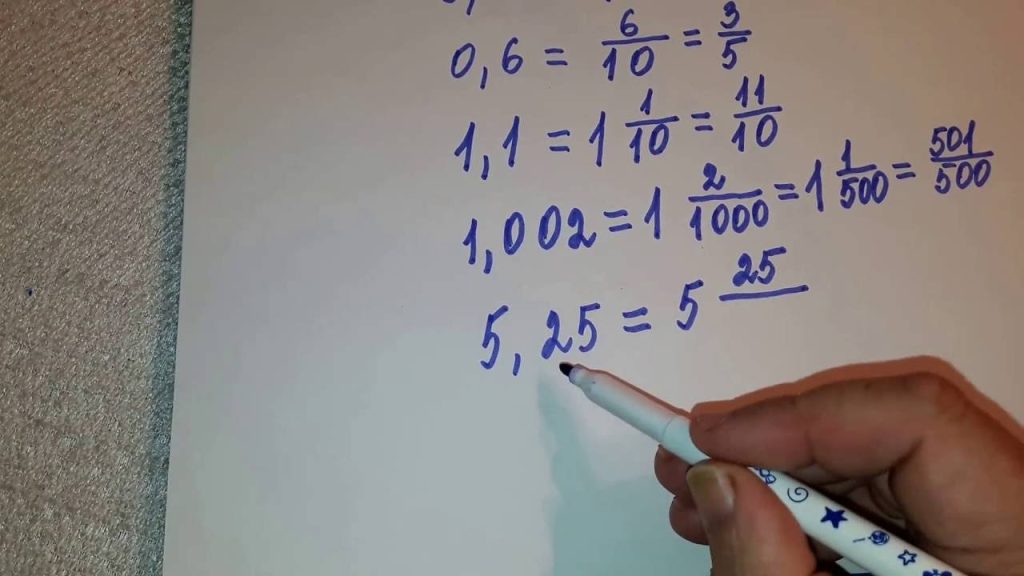





Залишити відповідь