Площа – це та невидима сила, яка визначає, скільки простору займає будь-яка поверхня, чи то листок паперу на вашому столі, чи величезне поле під сонцем. Уявіть, як фермер розраховує, скільки насіння висіяти на своєму лані, або архітектор малює план кімнати, де кожна деталь залежить від точного виміру. Простіше кажучи, площа вимірює розмір двовимірної фігури в квадратних одиницях, дозволяючи нам кількісно оцінити протяжність поверхонь. Це фундаментальна величина в математиці, яка виражає, наскільки “велика” поверхня, і її можна обчислити для найпростіших форм, як квадрат, чи складних кривих, як еліпс.
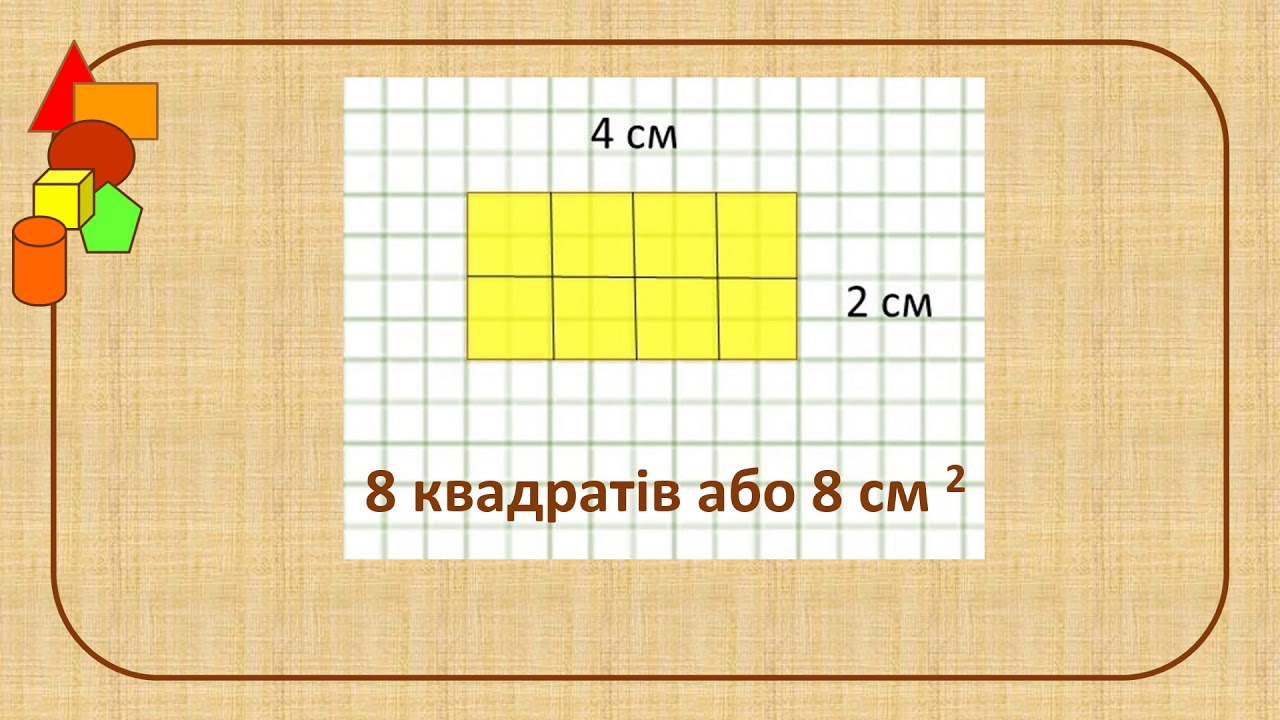
Коли ми говоримо про площу, то маємо на увазі кількість квадратних одиниць, що заповнюють фігуру без прогалин чи накладань. Наприклад, якщо квадрат зі стороною 1 метр має площу 1 квадратний метр, то прямокутник 2 на 3 метри охоплює 6 таких квадратів. Ця концепція не обмежується шкільними дошками – вона пронизує повсякденне життя, від розрахунку фарби для стін до моделювання кліматичних зон на картах. А тепер зануримося глибше, бо площа ховає в собі цілий світ відкриттів, від давніх цивілізацій до сучасних технологій.
Уявіть стародавнього єгиптянина, який після розливу Нілу перемірює свої поля, щоб справедливо розподілити землю. Саме такі практичні потреби народили поняття площі, роблячи її не просто абстракцією, а інструментом виживання. Сьогодні, у 2026 році, площа стає ключем до віртуальної реальності, де алгоритми обчислюють текстури об’єктів у реальному часі, роблячи ігри та симуляції неймовірно правдоподібними.
Історія поняття площі: від давнини до сучасності
Поняття площі сягає корінням у глибоку давнину, коли людство вперше зіткнулося з необхідністю вимірювати землю. У Стародавньому Єгипті, близько 3000 років до н.е., геометри – або “гарпедонапти”, як їх називали, – розробляли методи для розрахунку площ полів після щорічних повеней Нілу. Ці розливи стирали межі ділянок, і точне вимірювання ставало питанням справедливості та податків. За даними Вікіпедії, єгиптяни використовували прості формули для прямокутників і трикутників, що лягли в основу пізніших математичних систем.
Греки підняли це на новий рівень. Евклід у своєму трактаті “Начала” (близько 300 року до н.е.) систематизував знання про площі, вводячи аксіоми та теореми. Він показав, як обчислювати площі багатокутників, розділяючи їх на трикутники, і це стало основою евклідової геометрії. А Архімед, геній Сіракуз, пішов далі, наближаючи площі кривих фігур, як коло, методом вичерпування – предтечею сучасного інтегрального числення. Його розрахунки для кола з формулою πr² залишаються актуальними й досі, підтвердженими численними джерелами, включаючи математичні журнали як American Mathematical Monthly.
У Середньовіччі ісламські вчені, такі як Аль-Хорезмі, розвинули ці ідеї, інтегруючи їх з алгеброю. А в XVII столітті Рене Декарт і П’єр Ферма заклали основи аналітичної геометрії, де площа стала функцією координат. Йоганн Кеплер, обчислюючи площі для орбіт планет, наблизився до ідей інтегралів. Зрештою, Ісаак Ньютон і Готфрід Лейбніц у 1660-1670-х роках винайшли диференціальне та інтегральне числення, де площа під кривою обчислюється як інтеграл. Ця еволюція перетворила площу з практичного інструменту на потужний математичний концепт, який у 2026 році застосовується в комп’ютерному моделюванні та фізиці.
Сучасна історія додає шарів: у XX столітті Генрі Лебеґ розвинув теорію міри, узагальнюючи площу на складні множини, що важливо для ймовірностей і фракталів. Уявіть, як ці відкриття впливають на сьогоднішні технології – від GPS-карт, де площа визначає зони покриття, до штучного інтелекту, що аналізує зображення за площею об’єктів.
Одиниці вимірювання площі: від квадратних сантиметрів до гектарів
Одиниці площі – це як мова, на якій ми говоримо про розміри поверхонь, і вони варіюються залежно від масштабу. У метричній системі базовою є квадратний метр (м²), що дорівнює площі квадрата зі стороною 1 метр. Менші одиниці, як квадратний сантиметр (см²), ідеальні для вимірювання аркуша паперу, де 1 см² – це крихітний квадратик, що вміщує дрібні деталі. Більші, як гектар (10 000 м²), використовуються в сільському господарстві для полів, а квадратний кілометр (км²) – для територій країн.
У англо-саксонській системі панують квадратні дюйми, фути чи ярди, а акр (близько 4047 м²) – для земельних ділянок. Цікаво, як ці одиниці еволюціонували: гектар походить від грецького “hekaton” (сто), бо це 100 арів, а ар – від латинського “area”. За даними офіційних джерел, як сайт Міжнародного бюро мір і ваг, стандартизація відбулася в XIX столітті, забезпечуючи глобальну узгодженість.
Уявіть перехід між системами: щоб перетворити акри в гектари, множте на 0.4047. Це критично в міжнародній торгівлі, де помилка в одиницях може коштувати мільйонів. У 2026 році, з поширенням метричної системи, навіть США поступово переходять на м² для наукових цілей, роблячи обчислення універсальними.
Формули обчислення площі для основних геометричних фігур
Обчислення площі починається з простих фігур, де формули – як ключі до скарбниці. Для квадрата зі стороною a площа S = a², проста й елегантна, ніби ідеальний симетричний танок. Прямокутник розширює це: S = довжина × ширина, дозволяючи моделювати кімнати чи екрани гаджетів. Трикутник додає шарму з S = (основа × висота) / 2, де висота – перпендикуляр від вершини до основи, роблячи його універсальним для дахів чи вітрил.
Коло заворожує формулою S = πr², де π ≈ 3.14159, а r – радіус. Архімед наблизив це, вписуючи багатокутники, і сьогодні комп’ютери обчислюють π з мільйонами знаків для точності. Трапеція, з S = (сума паралельних сторін × висота) / 2, корисна в архітектурі для сходів чи доріг. А паралелограм? S = основа × висота, подібно до трикутника, але з паралельними сторонами, що імітує деформовані прямокутники.
Для складніших фігур, як еліпс, S = π × a × b, де a і b – півосі. Ці формули не просто числа – вони оживають у прикладах: площа футбольного поля (стандартно 7140 м²) визначає, скільки трави посіяти, а площа екрану смартфона впливає на комфорт перегляду. У 2026 році, з VR, обчислення площі кривих поверхонь стає щоденною справою для дизайнерів.
Приклади розрахунків з кроками
Давайте розберемо реальний приклад, щоб формули засяяли. Уявіть кімнату 4 м на 5 м – площа підлоги S = 4 × 5 = 20 м². Якщо додати трикутний альков з основою 3 м і висотою 2 м, то його площа 3 м², загальна – 23 м². Це допомагає розрахувати вартість ламінату, скажімо, по 500 грн/м², загалом 11 500 грн.
- Визначте форму: прямокутник плюс трикутник.
- Обчисліть кожну частину: прямокутник 20 м², трикутник (3 × 2)/2 = 3 м².
- Складіть: 23 м².
- Застосуйте: множте на ціну для бюджету.
Такий підхід робить математику живою, показуючи, як площа впливає на повсякденні рішення. У складніших випадках, як неправильний багатокутник, розділіть на трикутники – метод, що походить від Евкліда.
Просунуті методи обчислення площі: інтеграли та за межами
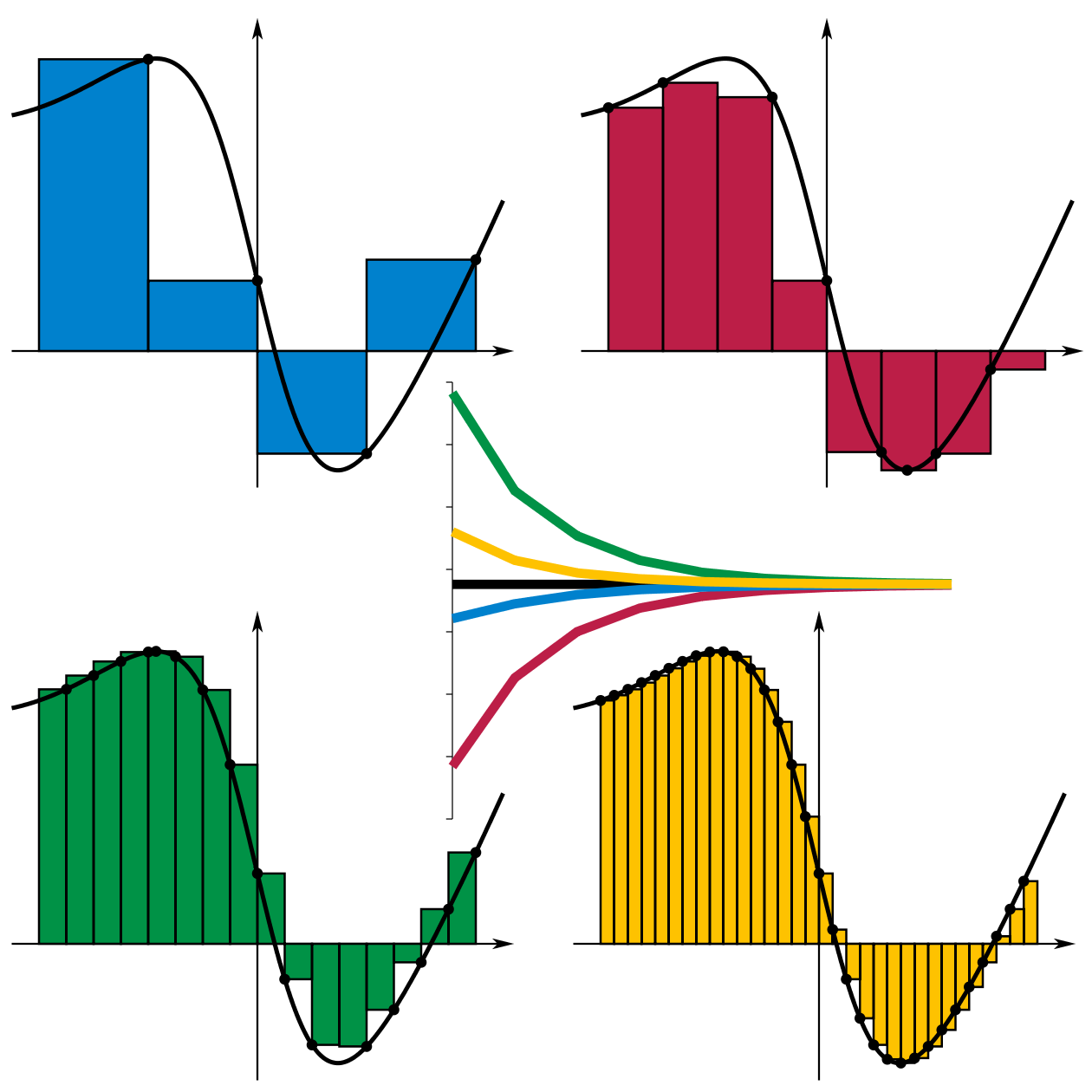
Коли фігури стають кривими, як парабола чи синусоїда, прості формули відступають, і на сцену виходить інтегральне числення. Інтеграл обчислює площу під кривою як межу сум Рімана – уявіть поділ на тонкі смужки, чия площа наближає загальну. Для функції f(x) від a до b, S = ∫_a^b f(x) dx. Це революціонізувало фізику: площа під графіком швидкості дає пройдений шлях.
У неевклідовій геометрії, як на сфері, площа викривлена – формула для сферичного трикутника враховує кривизну, важлива для астрономії. Фрактали, з нескінченно складними межами, мають “хаусдорфову” площу, що не збігається з класичною. У 2026 році, з квантовими комп’ютерами, алгоритми як Монте-Карло симулюють площі в багатовимірних просторах для машинного навчання.
Практично, в комп’ютерній графіці площа текстур обчислюється для рендерингу, роблячи віртуальні світи реалістичними. А в екології моделі площі лісів прогнозують зміни клімату, інтегруючи супутникові дані.
Застосування площі в реальному житті: від будівництва до технологій
Площа – не абстракція, а двигун прогресу. У будівництві вона визначає кількість матеріалів: для стіни 10 м² потрібно 10 літрів фарби при нормі 1 л/м². Фермери розраховують площі для іригації, оптимізуючи воду – в Україні, з її родючими землями, це критично для врожаїв. У медицині площа поверхні тіла (формула Дюбуа: S = 0.007184 × вага^0.425 × зріст^0.725) допомагає дозувати ліки.
У технологіях 2026 року площа сонячних панелей (ефективність до 25% на м²) визначає енергію домогосподарств. У дизайні веб-сайтів площа екрану впливає на UX, а в екології – на оцінку біорізноманіття, де площа заповідників корелює з видами. Навіть у мистецтві, як у картинах Мондріана, площа кольорових блоків створює баланс.
| Галузь | Приклад застосування | Типова площа |
|---|---|---|
| Будівництво | Розрахунок матеріалів для підлоги | 20-100 м² на кімнату |
| Сільське господарство | Площа посівів | 1-100 га на ферму |
| Технології | Площа екрану гаджетів | 100-500 см² |
| Медицина | Площа тіла для дозування | 1.5-2 м² для дорослого |
Ця таблиця ілюструє різноманітність, базуючись на даних з сайтів як Britannica та FAO. Після аналізу, видно, як площа з’єднує теорію з практикою, роблячи світ вимірюваним і керованим.
Цікаві факти про площу
Чи знали ви, що найбільша площа світу – Тяньаньмень у Пекіні – охоплює 440 000 м², здатна вмістити мільйон людей? Або що площа поверхні Землі становить близько 510 мільйонів км², з яких 71% – океани? У математиці “парадокс Банаха-Тарського” дозволяє розділити сферу на частини, що складаються в дві однакові сфери, кидаючи виклик інтуїтивному розумінню площі.
Ще один перлина: у фракталах, як сніжинка Коха, площа скінченна, але периметр нескінченний – дивовижний контраст! А в історії, Архімед так захопився обчисленням площі, що не помітив римських солдат, і його остання фраза була “Не чіпай моїх кіл!”. У 2026 році, з 3D-друком, площа шарів визначає міцність об’єктів, революціонізуючи виробництво.
Ці факти додають магії, показуючи, як площа – не суха цифра, а джерело чудес і відкриттів.
Типові помилки в обчисленні площі та як їх уникнути
Навіть досвідчені часом помиляються, плутаючи площу з периметром – площа всередині, периметр навколо. Інша пастка: забувати ділити на 2 у трикутнику, що призводить до подвоєння. Для кривих фігур наближення багатокутниками може бути неточним без достатньої кількості сторін.
- Плутанина одиниць: переплутати см² з м² – множте на 10 000 для перетворення.
- Ігнорування висоти: у паралелограмі висота, а не сторона, ключова.
- Неправильне використання π: заокруглення до 3 замість 3.14 зменшує точність на 4.7%.
- Для складних фігур: не розділяти на частини, що ускладнює розрахунок.
Щоб уникнути, завжди малюйте фігуру, перевіряйте одиниці та використовуйте калькулятори. У практиці, як у будівництві, помилка в площі може коштувати тисяч – краще перерахувати двічі.
Аналіз трендів: площа в еру цифровізації 2026
У 2026 році площа еволюціонує з цифровими технологіями. AI аналізує площі на супутникових знімках для моніторингу вирубки лісів, з точністю до 1 м². У метавсесвіті віртуальні площі продаються як NFT, вартістю мільйонів, перетворюючи абстракцію на актив.
Тренд – інтеграція з IoT: розумні будинки обчислюють площі кімнат для оптимального освітлення. У екології площа коралових рифів (зменшилася на 14% за десятиліття, за даними NOAA) сигналізує про кризу. Майбутнє – в квантових обчисленнях, де площа в багатовимірних просторах моделює нові матеріали.
Ці тренди роблять площу динамічною, пов’язаною з викликами сьогодення, від клімату до віртуальної економіки.





Залишити відповідь