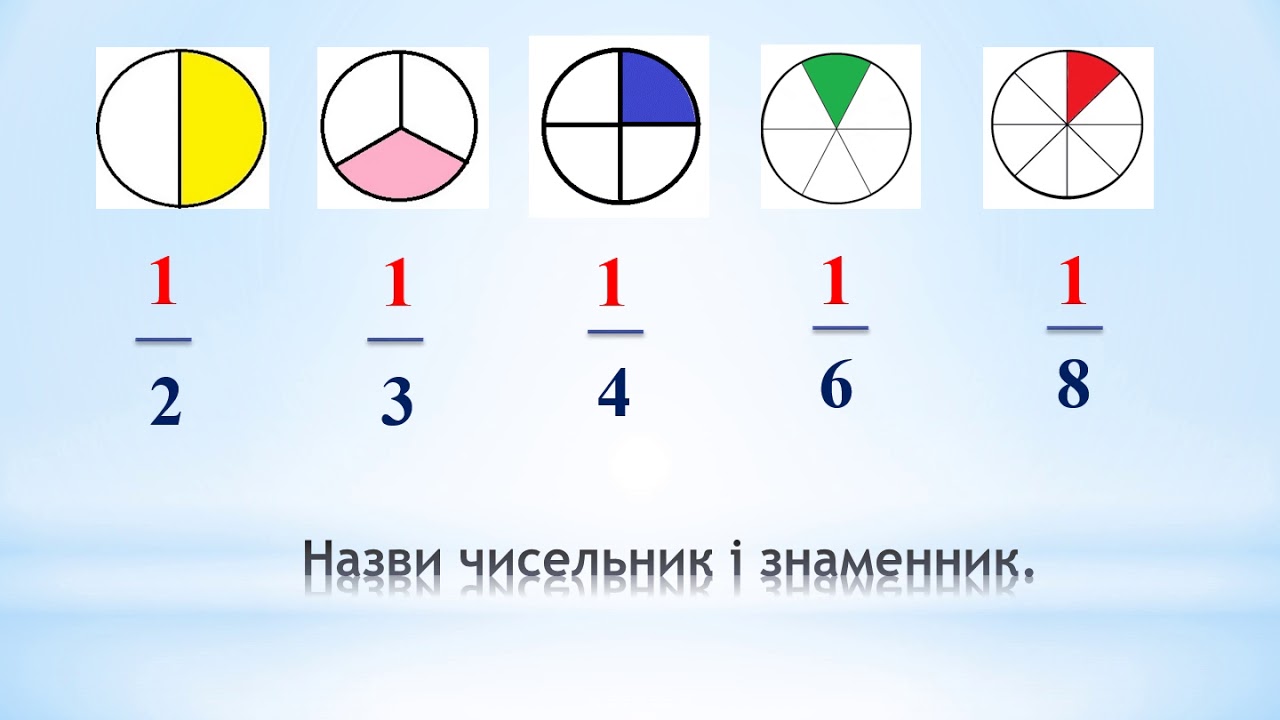
Коли ви ділили шоколадку на рівні частини з друзями і хтось забрав дві з чотирьох, це класичний дріб — 2/4, або спрощено 1/2. Дріб у математиці показує частку від цілого, результат ділення двох чисел, де верхнє число, чисельник, вказує, скільки частин узято, а нижнє, знаменник, — на скільки частин розбито ціле. Знаменник ніколи не буває нулем, бо ділити на нуль неможливо, інакше математика б зламалася, як комп’ютер без живлення.
Цей простий запис ховає в собі потужний інструмент, який древні цивілізації використовували для розподілу землі, а сьогодні ми застосовуємо в рецептах чи банківських відсотках. Розберемося, чому дріб — не просто шкільна нудьга, а ключ до розуміння світу, де все поділяється на частини.
Історія народження дробів: від пірамід до сучасних калькуляторів
Тисячі років тому, приблизно 4000 років тому, єгиптяни вже жонглювали дробами на папірусах. У папірусі Рінда, датованою 1650 роком до н.е., вони описували одиничні дроби на кшталт 1/2 чи 1/8 для вимірювання зерна чи площ полів. Цікаво, що більшість їхніх дробів мали чисельник 1 — сума таких “одиничок” замінювала складніші, ніби вони уникали повноцінних множинників зверху. Вавилоняни пішли далі: у шестидесятеричній системі (от звідки 60 хвилин в годині) вони записували дроби як пари клиновидів, досягаючи точності до 1/21600.
Греки, з їхньою любов’ю до геометрії, воліли уникати дробів, віддаючи перевагу пропорціям, але індійські математики в VI столітті ввели сучасніший запис. Китайці ще в III столітті н.е. експериментували з десятковими дробами для астрономії. Європа прокинулася пізно: італієць Фібоначчі в 1202 році в “Книзі абака” запровадив арабські (індійські) цифри з дробами, зробивши їх популярними за межами Сходу. А десяткові дроби прославив фламандець Сімон Стевін у 1585-му — його кома розділила ціле від дробової частини, полегшивши розрахунки для інженерів.
У Київській Русі VII століття дроби називали “ломаними числами”, і вони вважалися найскладнішим розділом арифметики. Сьогодні, у 2026 році, дроби еволюціонували в комп’ютерні алгоритми, де плаваюча кома імітує їх, хоч і з нюансами точності.
Розбір будови: чисельник, знаменник і риска між ними
Уявіть пиріг: знаменник — кількість шматків, на які його розрізали, чисельник — скільки ви з’їсте. У дробі 3/7 риска діє як знак ділення: 3 поділити на 7. Чисельник показує взяту частку, знаменник визначає розмір кожної частки. Якщо чисельник нуль, дріб дорівнює нулю — порожній шматок.
Основна властивість дробу — множення чисельника і знаменника на те саме число не змінює значення. Наприклад, 1/2 = 2/4 = 3/6. Це як розрізати пиріг дрібнішими шматками, але брати пропорційно більше. Скорочення навпаки: ділити на спільний дільник, щоб спростити, знайшовши найбільший спільний дільник (НСД).
Типи дробів: від простих до хитрих варіантів
Дроби не обмежуються шкільними прикладами — їх безліч форм для різних задач. Перед таблицею згадаймо: вибір типу залежить від контексту, від кулінарного рецепту до програмного коду.
| Тип дробу | Опис | Приклад | Коли використовувати |
|---|---|---|---|
| Правильний звичайний | Чисельник менший за знаменник, менше 1 | 3/4 | Частки від цілого, як половина яблука |
| Неправильний звичайний | Чисельник більший або рівний знаменнику, ≥1 | 5/4 | Коли частка перевищує ціле |
| Мішаний | Ціле число плюс правильний дріб | 1 1/4 | Зручний для великих значень, як 1 цілий плюс чверть |
| Десятковий | Знаменник — степінь 10, кома розділяє | 0,75 | Гроші, вимірювання |
| Алгебраїчний | Чисельник і знаменник — вирази з змінними | x/(x+1) | Рівняння, функції |
Дані з uk.wikipedia.org та ua.onlinemschool.com. Таблиця показує, як типи доповнюють один одного: неправильний легко перетворити в мішаний, поділивши чисельник на знаменник — ціла частина йде ліворуч, остача в новому дробі. Навпаки, мішаний множимо на знаменник для неправильного.
Операції з дробами: покрокові алгоритми з прикладами
Додавання і віднімання вимагають спільного знаменника — найменше спільне кратне (НСК). Ось вступ: спершу знайдіть НСК, перемножте чисельники і знаменники відповідним чином.
- Для 3/4 + 1/6: НСК(4,6)=12. 3/4=9/12 (×3), 1/6=2/12 (×2). Сума 11/12.
- Віднімання: 5/6 – 1/4. НСК=12. 10/12 – 3/12=7/12.
Потренуйтеся: помилки ховаються в неправильному НСК. Тепер множення — найпростіше, ніби ігноруєте риску.
- Добуток: 2/3 × 3/4 = 6/12 = 1/2. Скоротіть перед множенням для зручності.
- Для мішаних: 1 1/2 × 2 1/3. Перетворіть: 3/2 × 7/3 = 21/6 = 3 1/2.
Ділення — оберніть дільник і помножте: 3/4 ÷ 2/5 = 3/4 × 5/2 = 15/8. Логічно, бо ділення на частку — як множення на більшу порцію.
Десяткові дроби: місток до реального світу
Десятковий дріб — коли знаменник 10, 100 чи 1000. 0,25 = 25/100 = 1/4. Читання: дві десятитих, п’ять сотих. Перетворення: поділіть чисельник на знаменник. Зворотне — запишіть як 25/100, скоротіть.
У 2026-му вони панують у фінансах: 17,5% податку — це 0,175. Комп’ютери люблять їх, хоч 1/3 ≈ 0,333… йде в нескінченність, спричиняючи помилки в коді.
Практичні застосування: дроби скрізь навколо
У кулінарії рецепт на 4 порції: ви для двох — половина інгредієнтів, 1/2 склянки борошна. Фінанси: відсотки — 5% = 1/20, тож з 1000 грн 50 нарахують. У спорті: баскетболіст реалізував 7/10 штрафних — ефективність 70%.
Програмування: ймовірності в іграх чи AI-моделях — 0.7 шанс успіху. Будівництво: 3/8 дюйма гвинт. Навіть у музиці ноти — чвертні (1/4 такту). Без дробів світ був би цілим, але нудним.
Типові помилки початківців з дробами
Плутанина чисельника і знаменника: Думаєте, знаменник — скільки взяли? Ні, це частини цілого! Результат: переплутаний рецепт, де замість 1/2 візьмете 2/1 — весь торт.
- Додавання без спільного знаменника: 1/2 + 1/3 ≠ 2/5. Завжди НСК!
- Забуваєте скоротити: 2/4 лишаєте, а не 1/2 — числа розростаються.
- Ділення як віднімання: множення на обернене, не мінус.
- Неправильні на мішані без ділення: 7/2 ≠ 3 1/2? Поділіть!
Уникайте, практикуючи: візьміть пиріг, розріжте — і помилки зникнуть. Дані з уроків на miyklas.com.ua та houseofmath.com.
Алгебраїчні дроби додають перцю: x/ (2x+1), де змінні роблять їх динамічними для рівнянь. Скорочуйте, як (x^2-1)/(x-1) = x+1, якщо x≠1. Це основа вищої математики.
Дроби — не кінець, а початок: від єгипетських полів до нейромереж 2026-го, вони ділять світ на зрозумілі частки. Спробуйте в наступному рецепті чи бюджеті — відчуєте магію точності.
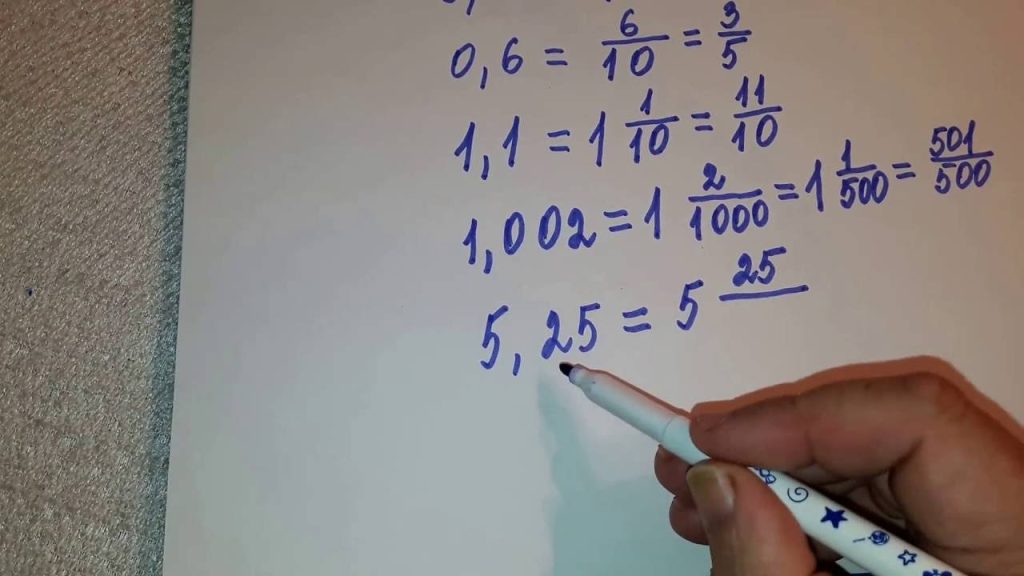





Залишити відповідь