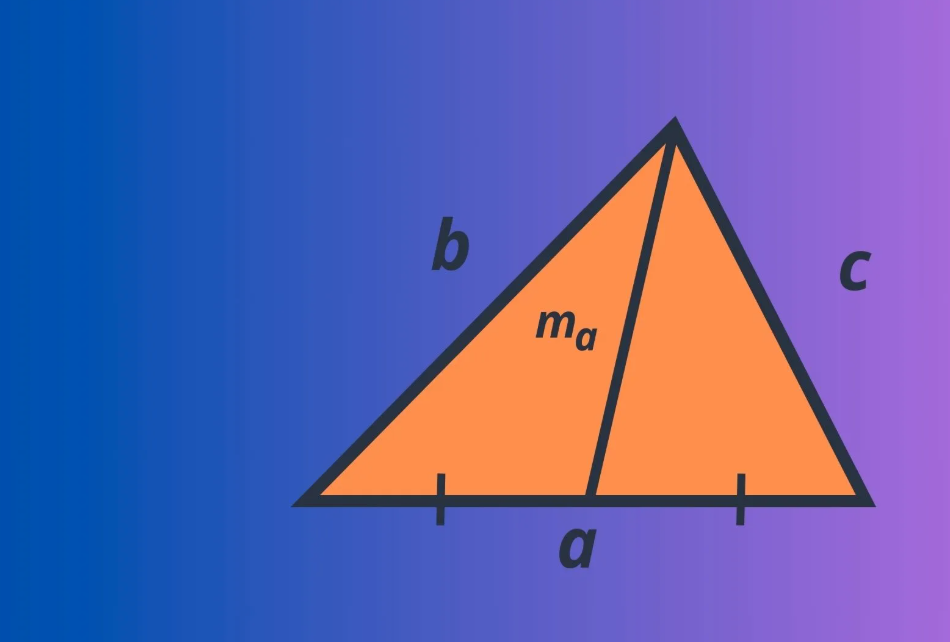
Уявіть трикутник, цю просту фігуру, що ховає в собі безліч таємниць, і ось одна з них – медіана, ніби невидимий місток, що з’єднує вершину з серединою протилежної сторони. Цей відрізок не просто лінія на папері; він уособлює баланс, розділяючи фігуру на частини рівної ваги. Медіана трикутника – це відрізок, проведений від вершини до середини протилежної сторони, і в кожному трикутнику таких медіан рівно три, кожна з яких несе свою унікальну роль у розумінні форми.
Коли ви проводите медіану, вона ніби розкриває внутрішню симетрію трикутника, дозволяючи нам зазирнути глибше в його структуру. Наприклад, у рівнобедреному трикутнику медіана з вершини до основи стає також висотою і бісектрисою, створюючи ідеальну гармонію. А в гострокутному чи тупокутному – вона поводиться по-іншому, але завжди зберігає ключові властивості, що роблять її незамінною в розрахунках.
Ця концепція не нова; вона корениться в давніх традиціях геометрії, де математики шукали способи описати світ через прості лінії. Медіана допомагає не тільки в шкільних задачах, але й у реальному житті, від архітектури до комп’ютерної графіки, де баланс форм визначає стабільність і красу.
Витоки поняття медіани в історії геометрії
Глибоко в античних текстах, де Евклід у своїх “Початках” близько 300 року до н.е. розбирав властивості трикутників, уже простежуються ідеї, що лягли в основу поняття медіани. Хоча сам термін “медіана” з’явився пізніше, від латинського “mediana” – середня, Евклід описував лінії, що з’єднують вершини з серединами сторін, вивчаючи їхню роль у балансі фігур. Ці ідеї розвивалися через століття, коли Архімед у III столітті до н.е. застосовував подібні концепції для обчислення центрів мас, що тісно пов’язано з точкою перетину медіан.
У середньовіччі арабські математики, такі як Аль-Хорезмі, розширювали евклідівські ідеї, інтегруючи їх у алгебру, що дозволило вивести формули для довжин медіан. А в епоху Відродження Леонардо да Вінчі використовував принципи медіан у своїх кресленнях, де баланс форм був ключем до реалістичних зображень. Сучасна геометрія, з її векторним підходом, остаточно сформувала розуміння медіани як вектора, що ділить трикутник на рівновагові частини.
Сьогодні, станом на 2026 рік, медіана вивчається не тільки в школах, але й у передових галузях, як-от робототехніка, де алгоритми балансування спираються на ці давні принципи. За даними математичних журналів, таких як “Journal of Geometry”, дослідження медіан еволюціонували до аналізу в багатовимірних просторах, де вони допомагають моделювати складні системи.
Основні властивості медіан трикутника
Медіани трикутника завжди перетинаються в одній точці, яку називають центроїдом, і це не випадковість, а фундаментальна властивість, що робить фігуру стійкою. Центроїд ділить кожну медіану в співвідношенні 2:1, де довша частина ближча до вершини, ніби підкреслюючи вагу кута. Ця точка – центр мас трикутника, де, якщо ви повісите картонну модель, вона ідеально збалансується.
Ще одна захоплива властивість: медіани розділяють трикутник на шість менших трикутників рівної площі, створюючи мозаїку рівноваги. У рівносторонньому трикутнику всі медіани рівні, і їхня довжина обчислюється просто, але в scalene, нерівносторонньому, кожна медіана унікальна, відображаючи асиметрію сторін. Крім того, якщо дві медіани перпендикулярні, то існує спеціальне співвідношення квадратів сторін, що додає шар інтриги до розрахунків.
Векторний погляд на медіани показує, що центроїд – це середнє арифметичне координат вершин, що робить його ідеальним для комп’ютерних симуляцій. У практиці це означає, що медіани допомагають у визначенні стабільності конструкцій, наприклад, у мостобудуванні, де баланс навантаження критичний.
Формули для обчислення довжини медіани
Довжина медіани – це не загадка, а точний розрахунок, заснований на сторонах трикутника. Для медіани m_a, проведеної до сторони a, формула звучить так: m_a = (1/2) √(2b² + 2c² – a²). Ця елегантна виразка, виведена з теореми Аполлонія, дозволяє швидко знайти довжину, знаючи лише сторони, і вона працює для будь-якого типу трикутника.
Розгляньмо приклад: у трикутнику зі сторонами 3, 4 і 5 (прямокутний), медіана до гіпотенузи 5 буде m = (1/2) √(2*3² + 2*4² – 5²) = (1/2) √(18 + 32 – 25) = (1/2) √25 = 2.5. Цікаво, що в прямокутному трикутнику медіана до гіпотенузи завжди дорівнює половині гіпотенузи, що є окремим випадком формули.
Якщо відомі всі три медіани, можна відновити сторони трикутника за формулою: a = (2/3) √(2m_b² + 2m_c² – m_a²). Це зворотна задача, корисна в інженерії, де вимірювання медіан може бути простішим, ніж прямих сторін. За даними сайту mathworld.wolfram.com, ці формули залишаються актуальними в 2026 році, з розширеннями для неевклідової геометрії.
Таблиця порівняння формул медіан для різних трикутників
| Тип трикутника | Формула медіани до сторони a | Приклад (сторони 3,4,5) |
|---|---|---|
| Рівносторонній | m = (√3/2) * сторона | Для сторони 3: m ≈ 2.598 |
| Прямокутний | m_a = (1/2) √(2b² + 2c² – a²) | До 5: m = 2.5 |
| Рівнобедрений | Залежить від основи | До основи 5: m ≈ 3.605 |
Ця таблиця ілюструє, як формули адаптуються до форми, роблячи обчислення гнучкими. Після вивчення таблиці стає зрозуміло, чому медіани – потужний інструмент для аналізу.
Побудова медіан і їх візуалізація
Щоб побудувати медіану, достатньо знайти середину сторони – це точка, де сторона ділиться навпіл, – і з’єднати її з протилежною вершиною. Уявіть, як олівець ковзає по паперу, створюючи цю лінію, що відразу ж розкриває центр трикутника. У програмному забезпеченні, як GeoGebra, це робиться кліком миші, але ручна побудова за допомогою циркуля додає чарівності процесу.
У різних трикутниках побудова варіюється: в гострокутному всі медіани всередині, в тупокутному одна може виходити за межі, але центроїд завжди внутрішній. Це властивість робить медіани універсальними для візуалізації балансу. Практичний приклад – у мистецтві орігамі, де складки уздовж медіан створюють симетричні фігури.
Експериментуйте самі: візьміть трикутник з координатами вершин (0,0), (4,0), (2,3), знайдіть середини і проведіть медіани – центроїд опиниться в (2,1), ідеально збалансований. Така візуалізація робить абстрактне поняття живим і зрозумілим.
Застосування медіан у реальному житті
Медіани виходять за межі підручників, проникаючи в архітектуру, де вони допомагають розраховувати центри мас будівель для стійкості. Уявіть Ейфелеву вежу: її структура спирається на принципи балансу, подібні до центроїда, щоб витримувати вітер. У комп’ютерній графіці медіани використовуються в алгоритмах триангуляції, де моделі об’єктів розділяються на трикутники для рендерингу.
У спорті, наприклад у біатлоні, траєкторії руху можуть моделюватися через медіани для оптимального балансу. А в медицині, при аналізі форм клітин, центроїд допомагає визначати аномалії. Навіть у повсякденному житті, коли ви ріжете піцу на рівні частини, медіани підказують, як знайти центр для рівномірного розподілу.
Сучасні додатки, станом на 2026 рік, включають дрони, де алгоритми стабілізації використовують векторні медіани для навігації. За даними журналу “Applied Mathematics”, такі застосування ростуть, роблячи медіани невід’ємною частиною технологій.
Порівняння медіан з бісектрисами та висотами
Медіана, бісектриса і висота – три сестри трикутника, кожна зі своєю місією. Медіана фокусується на серединах сторін, забезпечуючи баланс мас, тоді як бісектриса ділить кут навпіл, створюючи рівність кутів. Висота ж падає перпендикулярно, вимірюючи відстань для площі.
У рівнобедреному трикутнику вони часто збігаються, створюючи мультиінструмент, але в загальному випадку розходяться, кожна розповідаючи свою історію. Наприклад, точка перетину висот – ортоцентр – може бути поза трикутником, на відміну від завжди внутрішнього центроїда. Це порівняння підкреслює, чому медіана унікальна в своєму фокусі на рівновазі.
У задачах часто комбінують їх: знаючи висоту, можна знайти медіану для повного аналізу. Така взаємодія робить геометрію динамічною, де кожна лінія доповнює іншу.
Приклади обчислень медіан у різних типах трикутників
Візьмімо рівносторонній трикутник зі стороною 6: медіана дорівнює (√3/2)*6 ≈ 5.196, і всі три однакові, перетинаючись у центрі. Тепер scalene з сторонами 5,7,9: m до 5 = (1/2)√(2*7² + 2*9² – 5²) ≈ 6.874, показуючи асиметрію.
У прямокутному 3-4-5 медіана до 3: ≈2.958, до 4: ≈2.958, до 5: 2.5 – симетрія в асиметрії. Ці приклади ілюструють, як формули оживають, допомагаючи в реальних проєктах, як-от дизайн меблів для стабільності.
Ще один кейс: тупокутний з сторонами 2,3,4. Медіана до 4 ≈1.803, і центроїд все одно балансує фігуру. Такі розрахунки додають впевненості в розумінні.
Типові помилки при роботі з медіанами
Одна з поширених пасток – плутанина медіани з висотою: багато хто думає, що медіана завжди перпендикулярна, але це тільки в рівнобедреному випадку, що призводить до помилок у розрахунках площі.
Інша помилка – ігнорування співвідношення 2:1 при перетині; учні часто ділять медіану навпіл, забуваючи, що довша частина біля вершини, що спотворює координати центроїда.
При обчисленні довжини забувають помножити на 1/2 у формулі, отримуючи завищені значення. А в тупокутних трикутниках плутають, чи медіана виходить за межі, хоча центроїд завжди всередині. Уникаючи цих помилок, ви робите геометрію точнішою і приємнішою.
- Помилка в ідентифікації: Не плутайте медіану з бісектрисою – перша йде до середини сторони, друга ділить кут.
- Обчислювальна неточність: Завжди перевіряйте квадратний корінь у формулі, бо округлення може накопичувати помилки.
- Візуальна ілюзія: У малюнках медіани здаються рівними, але в нерівносторонніх вони різні – вимірюйте точно.
Ці типові помилки, якщо їх розпізнати, перетворюються на уроки, що посилюють розуміння медіан.
Розглядаючи ці аспекти, медіана постає не просто лінією, а ключем до глибшого сприйняття геометрії, що надихає на нові відкриття в повсякденних задачах і наукових проєктах.








Залишити відповідь