Квадрат стоїть на чолі простих геометричних фігур, де чотири рівні сторони зливаються з прямими кутами по 90 градусів, створюючи ідеальну симетрію. Ця замкнута форма не просто малюнок на папері — вона задає ритм усього, від плитки на підлозі до пікселів на екрані смартфона. Уявіть, як така проста конструкція стає фундаментом для складних конструкцій у архітектурі чи обчислень у комп’ютерах.
У геометрії квадрат визначається як чотирикутник, у якого всі сторони мають однакову довжину, а кожен кут дорівнює 90 градусам. Він поєднує в собі риси ромба й прямокутника, роблячи його унікальним представником правильних многокутників. Ця фігура належить до символу Шлефлі {4} і має діедральну групу симетрії D₄, що забезпечує чотири осі симетрії.
Простота квадрата приховує потужну логіку: задати його на площині достатньо двох суміжних вершин, а решта виводиться автоматично. Така точність робить квадрат незамінним у повсякденних розрахунках, від вимірювання кімнати до програмування ігор.
Визначення квадрата: від класичного до сучасного погляду
Класичне означення походить з античності: квадрат — це рівнобічний прямокутник або прямокутний ромб. У сучасній шкільній геометрії, як у 8-му класі НУШ, його називають паралелограмом з рівними сторонами та прямими кутами. Ця подвійність підкреслює, наскільки квадрат багатогранний — він успадковує властивості від кількох фігур одразу.
У координатній геометрії квадрат легко розмістити: наприклад, вершини в точках (0,0), (a,0), (a,a), (0,a), де a — сторона. Така побудова ідеальна для комп’ютерної графіки, де пікселі формують растрові зображення на основі квадратних комірок. Без квадрата не було б сучасних екранів з роздільною здатністю 4K чи Full HD.
Розрізняють одиничний квадрат зі стороною 1, який слугує базою для нормалізованих обчислень у математиці. Його площа дорівнює 1, а діагональ — √2, що часто використовується в доведеннях теорем.
Властивості квадрата: симетрія, що зачаровує
Квадрат переповнений симетрією, ніби природжений для гармонії. Протилежні сторони паралельні, діагоналі рівні між собою, перетинаються під прямим кутом і ділять одна одну навпіл. Кожна діагональ слугує бісектрисою кутів, а точка їхнього перетину — центром симетрії.
Навколо квадрата можна описати коло (радіус R = a√2 / 2), а в нього вписати коло (r = a/2). Сума внутрішніх кутів — 360°, як у будь-якого чотирикутника, але тут усе ідеально рівномірне. Ця перпендикулярність діагоналей робить квадрат єдиним чотирикутником з такою рисою серед паралелограмів.
Щоб глибше розібратися, розгляньмо порівняння з родичами:
| Фігура | Сторони | Кути | Діагоналі | Симетрія |
|---|---|---|---|---|
| Квадрат | Всі рівні | Всі 90° | Рівні, перпендикулярні, бісектриси | 4 осі, центр |
| Ромб | Всі рівні | Не обов’язково прямі | Перпендикулярні | 2 осі |
| Прямокутник | Протилежні рівні | Всі 90° | Рівні | 2 осі |
| Паралелограм | Протилежні рівні | Протилежні рівні | Не рівні | Центр |
Дані з uk.wikipedia.org. Після таблиці видно: квадрат — вершина еволюції чотирикутників, де властивості множаться. Ці риси полегшують доведення ознак: якщо чотирикутник — ромб із прямим кутом, то це квадрат.
Формули квадрата: практичні інструменти для розрахунків
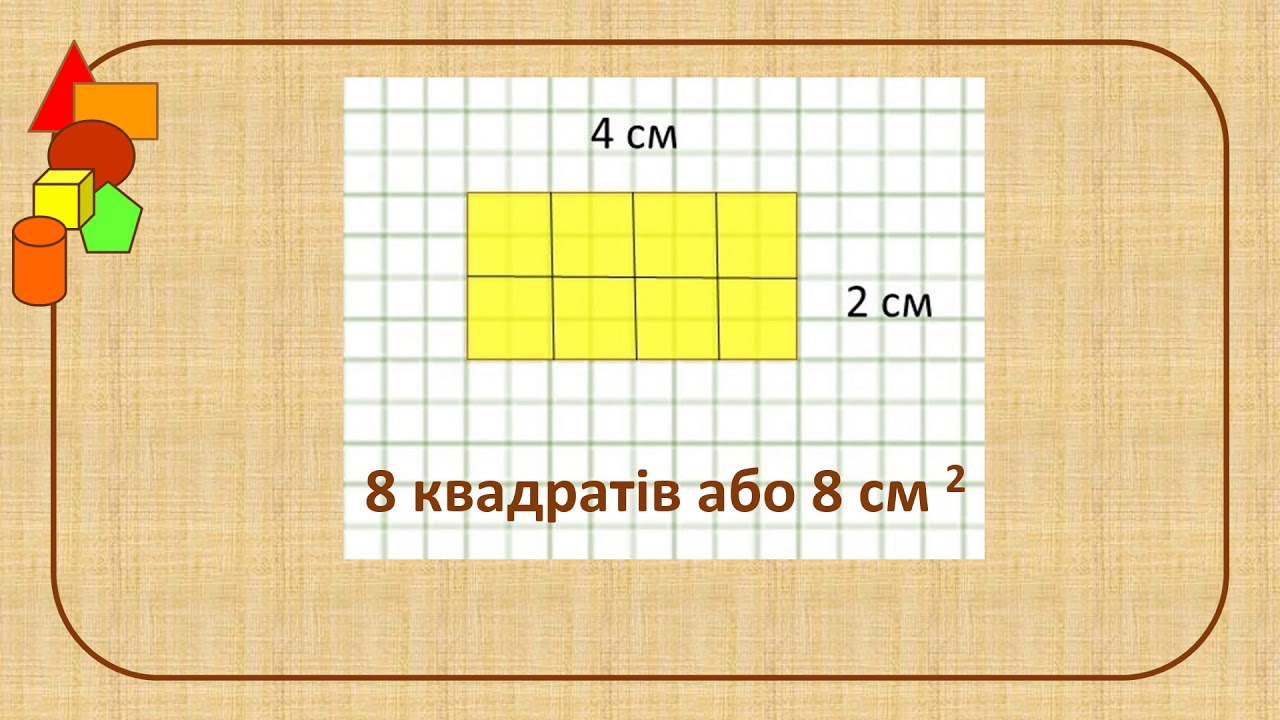
Обчислення з квадратом — справа проста й елегантна. Периметр P = 4a, де a — сторона; це сума всіх країв, корисна для паркану навколо городу. Площа S = a² — множення сторони на себе, як візуально заповнення одиничними квадратиками.
Діагональ d = a√2 виводиться з теореми Піфагора: у прямокутному трикутнику з катетами a і a гіпотенуза √(a² + a²). Приклад: для a=5 м периметр 20 м, площа 25 м², діагональ ≈7.07 м. Ця формула рятує інженерів при діагональному кріпленні конструкцій.
- Вимірте сторону a.
- Площа: помножте a на a.
- Діагональ: a помножте на √2 (≈1.414).
- Перевірте: для a=10, S=100, d≈14.14.
Ці кроки застосовуються в будівництві: квадратна плитка 30×30 см покриває 0.09 м². У 2026 році з ростом 3D-друку квадрати оптимізують матеріали для прототипів.
Історія квадрата: шлях від глибин тисячоліть
Квадрат з’явився в Вавилоні 2000 р. до н.е., де глиняні таблички фіксували його властивості для землемірства. Єгиптяни будували піраміди з квадратними основами, а в Індії ведичні тексти описували магічні квадрати. Евклід у “Началах” (бл. 300 р. до н.е., книга I, визначення 22) дав аксіоматичне означення, зробивши квадрат основою геометрії.
У Середньовіччі Аль-Хорезмі пов’язав квадрати з алгеброю, а Ренесанс приніс їх у мистецтво — Леонардо да Вінчі малював ідеальні пропорції. У 19 ст. Гаусс використав квадрати в теорії чисел, а Піфагор (VI ст. до н.е.) довів теорему з квадратами на сторонах прямокутного трикутника: площа на гіпотенузі дорівнює сумі на катетах.
Сучасність оживила квадрат: у 1915 Малевич намалював “Чорний квадрат”, символізуючи супрематизм. У комп’ютерах 1960-х пікселі стали квадратами, а в 2026 квантова графіка використовує їх для симуляцій.
Квадрат у алгебрі: від степеня до рівнянь
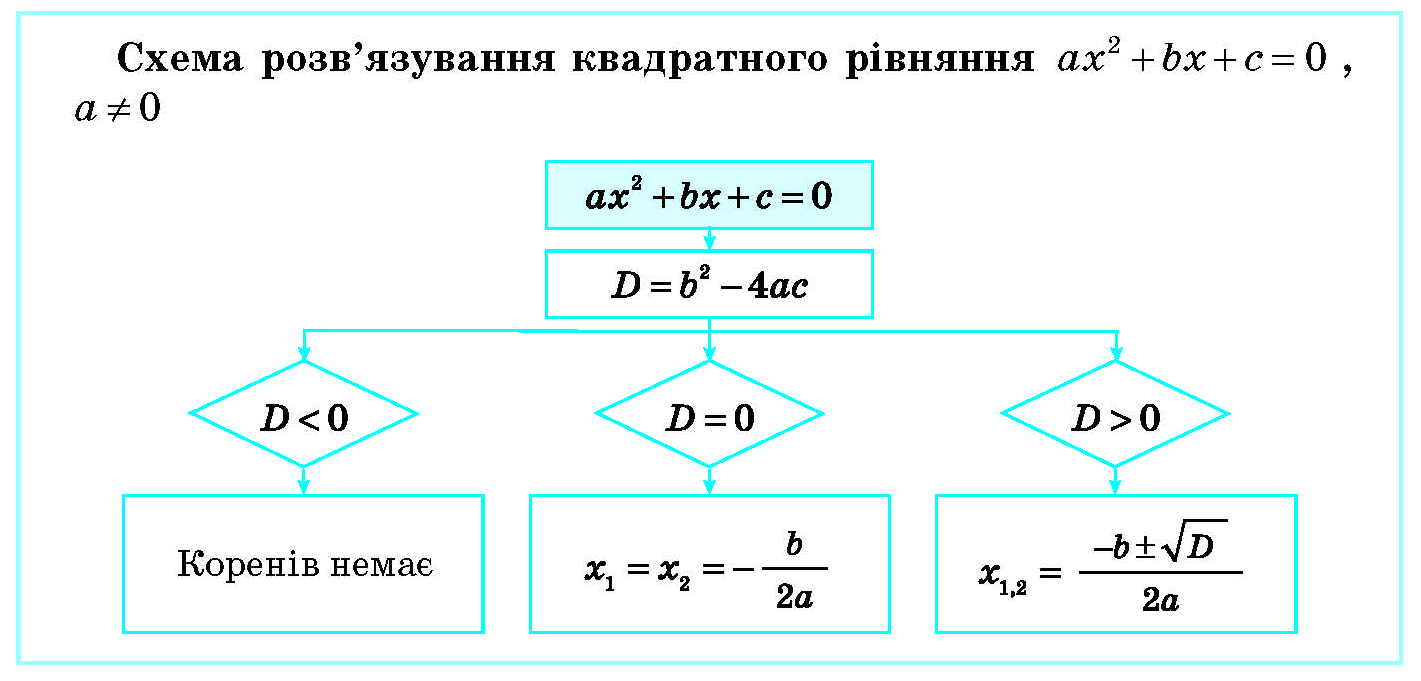
У алгебрі квадрат числа — це n² = n × n, друга степінь. Наприклад, 7²=49, сума перших 7 непарних чисел. Формула суми квадратів перших n чисел: n(n+1)(2n+1)/6. Квадратичні рівняння ax² + bx + c = 0 розв’язуються дискримінантом b²-4ac.
Комплексні числа розширюють: (a+bi)² = a² – b² + 2abi. У тригонометрії sin²φ + cos²φ = 1 — базова тотожність. Квадратні числа (1,4,9,16…) формують послідовність OEIS A000290, корисну в криптографії 2026 року.
Таблиця квадратів від 1 до 10: 1,4,9,16,25,36,49,64,81,100. Це інструмент для швидких обчислень, від шкільних задач до AI-моделей.
Застосування квадрата: від побуту до високих технологій
У архітектурі квадрати домінують у модульних системах: бетонні блоки, сонячні панелі. Плитка у ванній — класика, де S=a² оптимізує витрати. У мистецтві Казимир Малевич увічнив квадрат як чисту форму, вплинувши на мінімалізм.
Комп’ютерна графіка базується на квадратах: пікселі в растрі, вокселі в 3D. QR-коди — сітка квадратів для даних. У фізиці квадратна хвиля в електроніці, площа поверхонь у термодинаміці. У 2026 тренди: квадрати в метавсесвітах для будівництва віртуальних світів, де симетрія полегшує рендеринг.
У спорті квадратні ринги боксу, у кулінарії — форми випічки. Навіть у природі кристали солі наближаються до кубів — 3D-аналогів квадратів.
Цікаві факти про квадрат
- Магічний квадрат Ло Шу (Китай, 2800 р. до н.е.): 3×3 з числами 1-9, сума рядків 15. Використовувався в фен-шуй.
- Теорема Піфагора візуалізується квадратами: на катетах 3-4-5 площі 9+16=25.
- Найбільший квадрат на Землі — Соляні рівнини Бонневілль, США, сторона 10 км.
- У логіці “логічний квадрат” класифікує судження Арістотеля.
- Квадратна дірка в шахах: ферзь ходить як король + по діагоналі, використовуючи властивості.
Ці перлини показують, як квадрат пронизує культуру. Дані з uk.wikipedia.org.
Квадрат продовжує еволюціонувати: у нейромережах 2026 конволюційні шари обробляють квадратні фільтри для розпізнавання зображень. Його симетрія надихає дизайнерів на модульні меблі, а математиків — на нові теореми. Подивіться навколо: скільки квадратів ховається в вашому домі?






Залишити відповідь