Чотирикутник утворюється, коли чотири точки на площині з’єднуються прямими відрізками, формуючи просту замкнену ламану без самоперетинів. Ця базова геометрична конструкція має чотири вершини, чотири сторони та дві діагоналі, що сполучають протилежні кути. Сума внутрішніх кутів будь-якого простого чотирикутника завжди дорівнює 360 градусам, ніби чотири повні кола, розподілені рівномірно.
Вершини позначаються літерами, наприклад, ABCD, де A, B, C, D йдуть послідовно. Сусідні вершини з’єднані сторонами, протилежні — діагоналями AC та BD. Така структура робить чотирикутник фундаментом для складніших фігур, від прямокутних вікон у будинку до ромбів на спортивних полях. Розуміння цих елементів відкриває двері до глибоких властивостей, які архітектори та інженери застосовують щодня.
Опуклі чотирикутники тримають усі кути менше 180 градусів, діагоналі ховаються всередині, створюючи стабільну форму. Неопуклі ж дозволяють одному куту “зайти” за межу, ніби фігура згинається, а перехрещені нагадують метелика з крилами, що схрещуються. Ця різноманітність робить чотирикутники справжніми хамелеонами геометрії.
Елементи чотирикутника: від вершин до діагоналей
Кожна вершина — точка перетину двох сторін, де народжуються кути. Сторони, позначені довжинами a, b, c, d, визначають периметр як їхню суму. Діагоналі не лише розбивають фігуру на трикутники, але й несуть ключ до обчислень площі. Бімедіани, що з’єднують середини протилежних сторін, перетинаються в центроїді, додаючи симетрії навіть неправильним формам.
Кути бувають гострими, прямими чи тупими, але їхня сума фіксована — 360°. Уявіть, як ці елементи переплітаються в єдине ціле, подібно до каркасу надійного мосту. Без точного розуміння вершин і сторін неможливо перейти до класифікації, де чотирикутники набувають характеру.
Класифікація чотирикутників: ієрархія форм
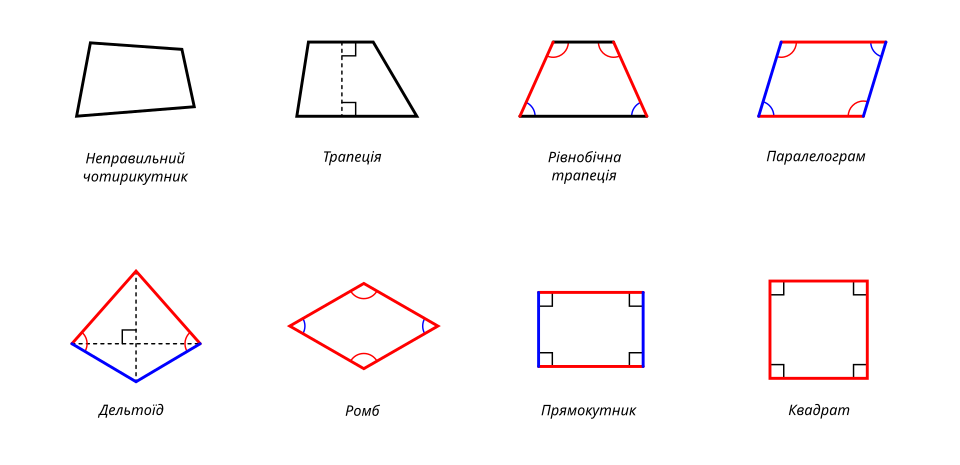
Чотирикутники поділяють за опуклістю, паралельністю сторін та симетрією. Опуклі домінують у повсякденності своєю стабільністю, тоді як увігнуті та перехрещені додають екзотики. Почніть з базових: неправильний чотирикутник без особливостей, просто чотири довільні сторони.
Трапеція: одна пара паралельних сторін
Трапеція вирізняється однією парою паралельних основ — нижньою довшою та верхньою коротшою, ніби дах будинку з нахиленими стінками. Рівнобічна трапеція ідеалізує форму: бічні сторони рівні, кути при основах симетричні, діагоналі однакової довжини. Площа рахується як середня основа помножена на висоту: S = (a + b)/2 * h, де a, b — основи.
У реальності трапеції всюди: від дорожніх знаків до крил комах. Ця простота робить її мостом до складніших паралелограмів.
Паралелограм: дві пари паралельних сторін
Паралелограм підносить симетрію на рівень вище — протилежні сторони рівні та паралельні, кути протилежні однакові. Діагоналі діляться навпіл у точці перетину. Площа проста: S = a * h або a * b * sin∠A, де a — основа, h — висота.
- Властивості: Протилежні кути рівні, суміжні — додаткові (180°).
- Ознаки: Дві протилежні сторони паралельні та рівні, або діагоналі ділять один одного навпіл.
- Приклад: Двері шафи, де ручки ковзають паралельно.
Ці риси роблять паралелограм основою для елітних типів, як ромб чи прямокутник.
Ромб, прямокутник, квадрат: вершина симетрії
Ромб — паралелограм з рівними сторонами, діагоналі перпендикулярні та бісектриці кутів. Площа: S = d1 * d2 / 2, де d1, d2 — діагоналі. Прямокутник додає прямі кути, діагоналі рівні: S = a * b. Квадрат поєднує все — рівні сторони, прямі кути, діагоналі рівні та перпендикулярні: S = a².
Ромби мерехтять у бейсбольних полях, прямокутники формують екрани смартфонів, квадрати викладають плитку. Кожен еволюціонує від попереднього, накопичуючи досконалість.
Спеціальні чотирикутники: описані та вписані
Описаний чотирикутник (вписане коло) задовольняє теорему Пітака: суми протилежних сторін рівні (a + c = b + d). Вписаний (описане коло) — суми протилежних кутів по 180°. Біцентричний комбінує обидва, ідеал гармонії.
Ортодіагональний з перпендикулярними діагоналями нагадує дельтаплан, площу рахуйте як половину добутку діагоналей.
Властивості чотирикутників, що вражають уяву
Сума кутів — 360° для опуклих, бо чотирикутник розбивається на два трикутники з сумою 180° кожен. Діагоналі в паралелограмі діляться порівну, у ромбі стикаються під 90°. Бімедіани утворюють “внутрішній каркас”, їх довжини пов’язані з діагоналями: p² + q² = 2(m² + n²).
Теорема Варіньона перетворює будь-який чотирикутник на паралелограм: середини сторін стають його вершинами, сторони паралельні діагоналям оригіналу. Площа Варіньонового паралелограма — половина площі чотирикутника, ніби дзеркальне відображення.
Формули площі чотирикутників: від простого до складного
Для спеціальних типів формули інтуїтивні, але загальний випадок вимагає хитрощів. Бретшнейдера узагальнює Герона: S = √[(s-a)(s-b)(s-c)(s-d) – abcd cos²((A+C)/2)], де s — напівпериметр. Для ортодіагональних: S = (d1 * d2)/2.
| Тип чотирикутника | Формула площі | Приклад |
|---|---|---|
| Паралелограм | S = a * b * sin∠A | Сторони 5, 3, ∠60°: S=7.5 |
| Трапеція | S = (a+b)/2 * h | Основи 4,6, h=2: S=10 |
| Ромб | S = d1*d2/2 | Діагоналі 4,6: S=12 |
| Квадрат | S = a² | a=5: S=25 |
| Загальний опуклий (Бретшнейдер) | S = √[(s-a)(s-b)(s-c)(s-d) – abcd cos²((A+C)/2)] | Для вписаного спрощується до Брамагупти |
Джерела даних: uk.wikipedia.org, mathworld.wolfram.com.
Векторний спосіб: S = ½ |AC × BD|, ідеальний для координат. Ці формули перетворюють абстракцію на інструмент для інженерів.
Цікаві факти про чотирикутники
- Паралелограм Варіньона існує для будь-якого чотирикутника, навіть перехрещеного — завжди паралелограм!
- У квадрата діагоналі не лише рівні, а й слугують осі симетрії, роблячи його королем симетрії.
- Теорема Птолемея для вписаного: добуток діагоналей дорівнює сумі добутків протилежних сторін (pq = ac + bd).
- Найбільша площа для фіксованого периметру — у квадрата, ніби природа прагне досконалості.
- У просторовій геометрії чотирикутники утворюють тетраедри з діагоналями як ребрами.
Ці перлини роблять геометрію живою наукою, повною сюрпризів.
Чотирикутники в реальному світі: від архітектури до спорту
Прямокутники домінують у будівлях — стіни, вікна, двері забезпечують міцність і простір. Ромби прикрашають мозаїки Парфенона чи сучасні фасади, додаючи динаміки. Трапеції формують похилі дахи, розподіляючи навантаження снігу ефективніше.
- У спорті: бейсбольне поле — ромб з кутами 90°/60° для оптимальної гри.
- Повсякденне: конверт — трапеція для компактності; монітор — прямокутник для чіткості зображення.
- Архітектура: Ейфелева вежа використовує трапецієподібні секції для стійкості; готичні арки базуються на чотирикутних рамах.
- Природа: крила метелика наближаються до перехрещених чотирикутників для аеродинаміки.
- Графіка: пікселі — квадрати, що будують цифровий світ.
Архітектори обирають ромби для мостів, бо діагоналі розподіляють сили рівномірно. У 2025 році 3D-друк використовує параметричні чотирикутники для оптимізації структур, зменшуючи вагу на 30% (за даними Autodesk research).
Теореми, що розкривають магію чотирикутників
Теорема Варіньона перетворює хаос у порядок: середини сторін завжди дають паралелограм. Пітака для описаних: a + c = b + d, проста умова для вписаного кола. Бретшнейдер узагальнює площу, враховуючи кути.
Птолемей для вписаних: ac + bd = pq, зв’язок сторін і діагоналей. Ці теореми, виведені Евклідом та його послідовниками, лежать в основі CAD-програм, де моделі будуються на чотирикутних сітках.
Ейлер довів: a² + b² + c² + d² = p² + q² + 4x², де x — відстань між серединами діагоналей. Такі рівності перетворюють геометрію на точну науку, готову до викликів сучасності.














Залишити відповідь