Корінь рівняння ховається в серці будь-якої математичної загадки — це те значення змінної, яке перетворює хаотичний вираз на чисту істину, де ліва частина ідеально дорівнює правій. Підставте число 2 у просте рівняння 2x + 3 = 7, і отримаєте 7 = 7 — магія збігу! Для початківців це як ключ, що відчиняє двері, а для просунутих — інструмент, який розкриває таємниці складних систем від фізики до економіки.
Уявіть рівняння як битву двох сторін: одна намагається переважити, інша тримається. Корінь змушує їх стати рівними, ніби дипломат, що мирить супротивників. Цей базовий принцип лежить в основі всього — від шкільних задачок до моделювання клімату чи траєкторій ракет.
Графічний сенс кореня рівняння
Графік функції перетворює абстрактне рівняння на живу картину. Корінь рівняння f(x) = 0 — це точка, де крива перетинає вісь абсцис, ніби стріла, що влучає в мішень. Для параболи y = x² – 4 два перетини дають корені x = 2 і x = -2, а якщо парабола не торкається осі, як у y = x² + 1, реальних коренів немає — тільки уявні світи комплексних чисел.
Цей візуальний підхід полегшує розуміння множинності коренів. Кількість перетинів з віссю x показує, скільки розв’язків має рівняння: один для дотичної, нуль для промаху, два чи більше для хитрих хвиль синуса чи косинуса. Графічно корінь — це x-інтерсепт, момент нульової висоти на карті функції.
У реальному житті графіки оживають: траєкторія польоту м’яча моделюється параболою, і корінь показує час повернення на землю. Побудуйте графік у GeoGebra чи Desmos — і рівняння перестає бути сухою формулою, стаючи динамічною історією.
Корені лінійних рівнянь: простота сили
Лінійні рівняння ax + b = 0 — це прямі лінії на графіку, завжди з одним коренем x = -b/a, якщо a ≠ 0. Розв’яжіть 3x – 6 = 0: x = 2, перевірте підстановкою — чиста логіка без сюрпризів. Такі рівняння панують у повсякденності: розрахунок швидкості v = s/t чи баланс бюджету доходи – витрати = 0.
- Перенесіть члени з протилежним знаком: зліва — змінні, справа — константи.
- Поділите на коефіцієнт при x, уникаючи ділення на нуль, бо це веде до абсурду 0=1.
- Перевірте: підставте назад, ніби тест-драйв автомобіля перед покупкою.
Цей метод еквівалентний — не втрачає і не додає коренів. У фізиці рівняння F = ma дає прискорення a = F/m, де корінь миттєво вирішує задачу для інженерів. Простота лінійних рівнянь робить їх фундаментом для складніших конструкцій.
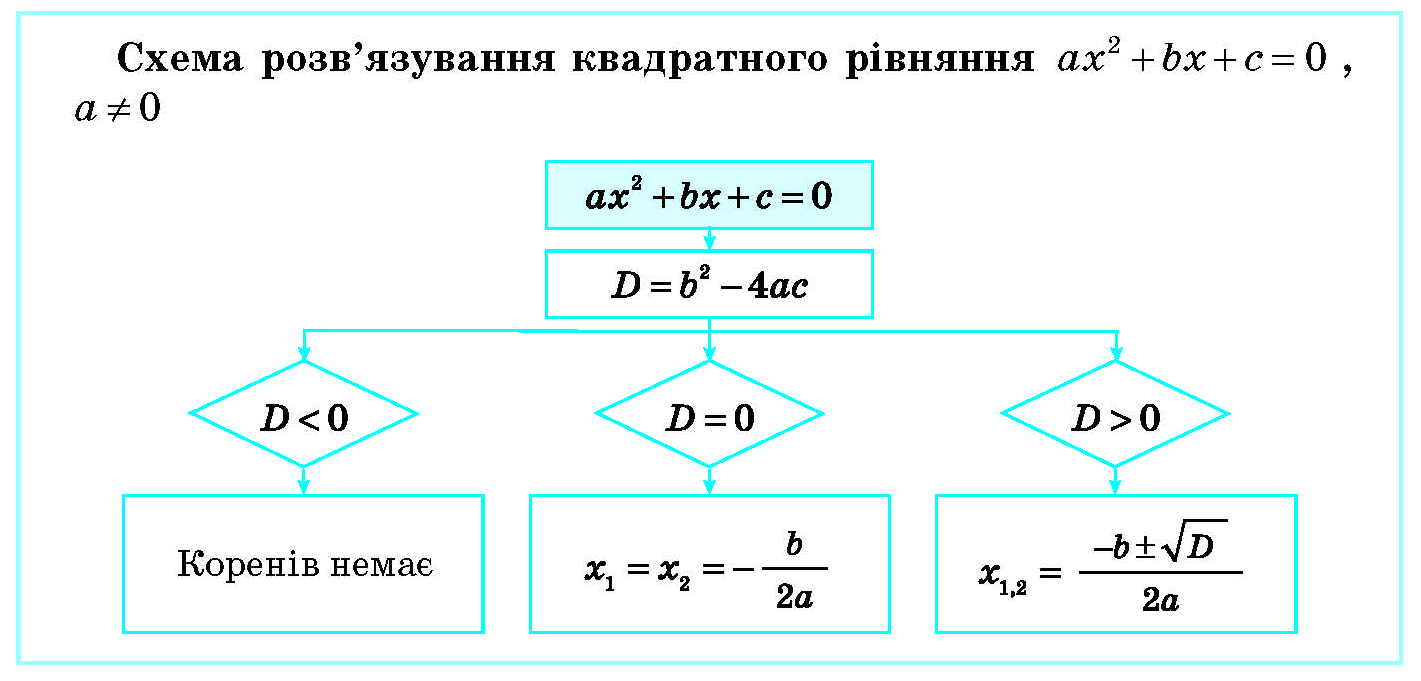
Квадратні рівняння: дискримінант вирішує долю
Квадратні рівняння ax² + bx + c = 0 кидають виклик формулою x = [-b ± √(b² – 4ac)] / (2a), де дискримінант D = b² – 4ac — суддя. Якщо D > 0, два реальних корені; D = 0 — один подвоєний; D < 0 — втеча в комплексні числа. Візьміть x² – 5x + 6 = 0: D = 25 – 24 = 1, корені (5 ± 1)/2 = 3 і 2 — ідеальні цілі числа.
| Значення D | Кількість реальних коренів | Приклад | Корені |
|---|---|---|---|
| D > 0 | Два різні | x² – 3x + 2 = 0 | x=1, x=2 |
| D = 0 | Один (кратний) | x² – 4x + 4 = 0 | x=2 |
| D < 0 | Немає (комплексні) | x² + 1 = 0 | x=±i |
Таблиця базується на стандартних властивостях з uk.wikipedia.org. Альтернативи: факторизація (x-2)(x-3)=0 чи графік параболи. У бізнесі модель прибутку P = -x² + 10x – 9 знаходить максимум при вершині, а корені — точки беззбитковості.
Історія додає шарму: вавилоняни 4000 років тому розв’язували геометрично, а Брахмагупта у VII ст. дав повну формулу. Сьогодні це основа для ракетних траєкторій чи оптимізації логістики.
Вищі степені, комплексні корені та кратність
Поліноми вищого степеня, як x³ – 6x² + 11x – 6 = 0, факторизуються на (x-1)(x-2)(x-3)=0 з коренями 1,2,3. Теорема Безу допомагає ділити, знаходячи раціональні корені. Кратність — скільки разів корінь повторюється: у (x-1)²(x-2)=0 корінь 1 кратний 2, графічно — дотична до осі.
Комплексні корені приходять парами для дійсних коефіцієнтів: x² + 2x + 2 = 0 дає x = -1 ± i. Вони описують коливання пружини в фізиці чи хвилі в електроніці — реальні явища з уявними числами. Без комплексних чисел квантова механіка була б неможливою.
Трансцендентні рівняння, як sin(x) = x/π, не мають закритої форми — тут вступають чисельні методи. Економісти моделюють попит D = 100 – 2P = пропозиція S = 20 + 3P, розв’язуючи 80 = 5P, P=16 — рівноважна ціна.
Чисельні методи: коли алгебра пасує
Метод бісекції ріже інтервал навпіл, де знак функції змінюється, наближаючись до кореня. Для cos(x) – x = 0 на [0,1]: середина 0.5, f(0.5)>0, ріжте праву половину — ітеративно до точності 0.001. Повільно, але надійно, як черепаха, що завжди фінішує.
- Знайдіть інтервал [a,b] з f(a)*f(b) < 0.
- c = (a+b)/2, перевірте знак.
- Повторюйте, доки |b-a| < ε.
Метод Ньютона блискавичний: x_{n+1} = x_n – f(x_n)/f'(x_n), використовує дотичну. Для e^x – 3x² = 0 з x0=0.5: похідна e^x – 6x, наступний x1 ≈ 0. something — сходиться квадратично. Ідеально для інженерії, де секунди рахують (джерело: mathworld.wolfram.com).
Ці методи рятують у програмуванні: Python з SciPy знаходить корені за мілісекунди. У 2025 році нейромережі прискорюють пошук для хаотичних систем.
Типові помилки при пошуку коренів рівнянь
Найпоширеніша пастка — сторонні корені в ірраціональних рівняннях. √(x+1) = -1 здається розв’язком після квадрату x+1=1, x=0, але корінь не буває від’ємним! Завжди перевіряйте ОДЗ і підстановкою.
- Забули знак при дискримінанті: для D<0 кажуть “немає коренів”, ігноруючи комплексні.
- Ділення на (x-a) без перевірки кратності — втрата розв’язку.
- У тригонометрії: sin(x)=0.5 дає x=π/6 + 2kπ, але забувають загальний вигляд.
- Перенесення в ірраціональних без ізоляції: призводить до extraneous roots.
Гумор у тому, що комп’ютер видасть “помилка”, а ви втратите годину. Порада: тестуйте корені, ніби детектив перевіряє алібі. Згідно з уроками на Khan Academy, 40% помилок — від не-перевірки.
Корені рівнянь — це не просто числа, а ключі до реальності: від прогнозу попиту в 2026 році до симуляції клімату. Експериментуйте з калькуляторами, будуйте графіки — і математика засяє новими барвами, манячи глибше в нескінченні можливості.














Залишити відповідь