На числовій прямій точка з координатою мінус три ховається ліворуч від нуля, але її відстань до початку відліку така ж, як у точки плюс три праворуч. Ця відстань і є модулем числа — простим, але потужним інструментом, що стирає знак, лишаючи лише величину. Уявіть нескінченну лінію чисел, де модуль діє як нейтральний арбітр, перетворюючи будь-яке число на його “позитивний двійник”.
У шкільних підручниках модуль вводять для раціональних чисел, але його сила розкривається в аналітичній геометрії, фізиці та навіть коді програм. Він не просто правило обчислень — це фундамент відстаней у просторі, норми векторів і критеріїв похибок. Розберемося крок за кроком, від бази до глибин.
Геометричний сенс: відстань, що не залежить від напрямку
Коли ви малюєте числову пряму, нуль стоїть посередині, додатні числа розбігаються праворуч, від’ємні — ліворуч. Модуль числа a — це довжина відрізка від нуля до точки a, незалежно від сторони. Для a = 5 це п’ять одиниць праворуч, для a = -5 — п’ять ліворуч. Результат завжди невід’ємний.
Цей сенс оживає в задачах на відстані між точками. Формула проста: відстань між A і B дорівнює |A – B|. Візьміть A = -2, B = 3: | -2 – 3 | = | -5 | = 5. Ліворуч чи праворуч — байдуже, модуль фіксує метраж.
Уявіть прогулянку: ви пройшли 4 км на схід (+4), потім 6 км на захід (-6). Загальний зсув — |4 + (-6)| = | -2 | = 2 км на захід, але загальна відстань пройденого шляху — 4 + 6 = 10 км. Модуль тут розрізняє зсув від витраченого.
Формальне визначення та як його обчислювати
Модуль позначають вертикальними рисками: |a|. За означенням з uk.wikipedia.org:
|a| = a, якщо a ≥ 0; |a| = -a, якщо a < 0.
Для нуля |0| = 0 — очевидна точка на початку. Альтернативно, |a| = √(a²), бо квадрат стирає знак, а корінь повертає додатне. Обчислення елементарне: візьміть | -7.3 | = 7.3, |3.14| = 3.14. Складніше з виразами: |2x – 5|, де спершу підставляєте значення, потім знак модуля.
| Число a | |a| | Пояснення |
|---|---|---|
| 5 | 5 | Додатне, лишаємо як є |
| -8 | 8 | Від’ємне, міняємо знак |
| 0 | 0 | Нуль — фіксована точка |
| 2.5 | 2.5 | Дробове додатне |
| -1/3 | 1/3 | Раціональне від’ємне |
Таблиця базується на стандартних прикладах з математичних посібників, як-от bankchart.com.ua. Після обчислень переходьте до властивостей — вони спрощують роботу з виразами.
Властивості модуля: правила, що економлять час
Модуль поводиться як дисциплінований солдат: завжди ≥ 0, множиться акуратно, додається з обережністю. Ось ключові властивості для дійсних чисел a, b:
- Невід’ємність: |a| ≥ 0, з рівністю тільки при a=0. Доказ: з означення, відстань не буває від’ємною.
- Мультиплікативність: |ab| = |a| · |b|. Приклад: | -3 · 4 | = | -12 | = 12, а 3 · 4 = 12. Доказ: квадрати множаться, корені теж.
- Нерівність трикутника: |a + b| ≤ |a| + |b|. “Прямий шлях коротший за зигзаг”. Доказ: оберіть знак s=±1 так, щоб s(a+b)=|a+b|, тоді s a ≤ |a| тощо.
- Обернена: |a – b| ≥ ||a| – |b||. Корисно для оцінок похибок.
- Ідемпотентність: ||a|| = |a| — подвійний модуль марний.
Ці правила перетворюють громіздкі вирази на елегантні. Наприклад, у |3x – 2| + |x + 1| для великого x це ≈ |3x| + |x| = 4|x|. Перед списком я наголосив на базі, а тепер додам: у нерівностях |a| ≤ c (де c≥0) еквівалентно –c ≤ a ≤ c.
Рівняння та нерівності: розкриваємо “коробки”
Рівняння з модулем нагадують детектив: |x – 2| = 4 означає відстань від x до 2 дорівнює 4, тож x=6 або x=-2. Кроки: розкрийте як x-2=4 чи x-2=-4.
- Визначте критичні точки, де вираз під модулем нуль (корені).
- Розбийте числову пряму на інтервали.
- На кожному інтервалі зніміть модуль, розв’яжіть, перевірте.
Приклад нерівності: |2x + 1| < 5. Критична точка x=-0.5. Інтервали: x < -0.5 (2x+1<0, тож -(2x+1)<5 → 2x+1 > -5 → x > -3), -0.5 ≤ x (2x+1 ≥0, 2x+1 <5 → x<2). Рішення: -3 < x < 2.
Складніше: |x – 1| + |x + 1| = 4. Мінімум суми — 2 (при -1≤x≤1), тож розв’язків немає. Перевірте графіком — V-подібні “літери” зливаються в трапецію.
Модуль за межами дійсних: комплексні числа та вектори
Для комплексного z = x + iy: |z| = √(x² + y²) — відстань до початку в площині. Приклад: |3 + 4i| = 5, бо 3-4-5 трикутник. Властивості аналогічні, нерівність трикутника узагальнюється на суми.
У векторах евклідова норма ‖v‖ = √(∑ v_i²) — це модуль у многомерному просторі. Для R³: ‖(1, -2, 3)‖ ≈ 3.74. У програмуванні це distance в графіці чи машинному навчанні.
Застосування: від фізики до коду та фінансів
У фізиці швидкість — модуль вектора швидкості, |v|, незалежно від напрямку. Вимірювання похибки: |обчислене – точне|. У Python функція abs() для int, float, комплексних — універсал.
print(abs(-7)) # 7 print(abs(3 + 4j)) # 5.0
Економіка: абсолютна похибка прогнозу продажів |фактичне – прогноз|. У 2025 році в AI-моделях модуль у втраті MAE (Mean Absolute Error) для регресії. Графіка: відстань пікселів |dx| + |dy| у Манхеттенській метриці.
Цікаві факти про модуль числа
- Термін “модуль” ввів Жан-Робер Арганд 1806 для комплексних, позначення |x| — Карл Вейєрштрасс 1841 (з en.wikipedia.org).
- У Римі використовували без знака для відстаней, але формально — з 17 ст. у роботах Декарта.
- Модуль нуль — єдиний фіксований пункт, бо |0| = 0.
- У p-нормах (p=1: сума |x_i|, p=∞: max |x_i|) — інструмент data science 2025.
- Графік y=|sin x| створює “хвилі” без дна — популярний у візуалізаціях.
Типова помилка новачків — забути перевіряти розв’язки після розкриття модуля, бо позамежні “мусора”. Або плутати з modulo (%) — остачею. У рівняннях множинних модулів шукайте медіану точок.
Модуль числа пронизує математику, як коріння дерева — всю крону застосувань. Спробуйте самі: запрограмуйте калькулятор abs() чи змоделюйте траєкторію з |Δx|. Це не кінець — попереду норми в тензорах та квантова механіка, де |ψ|² — імовірність.
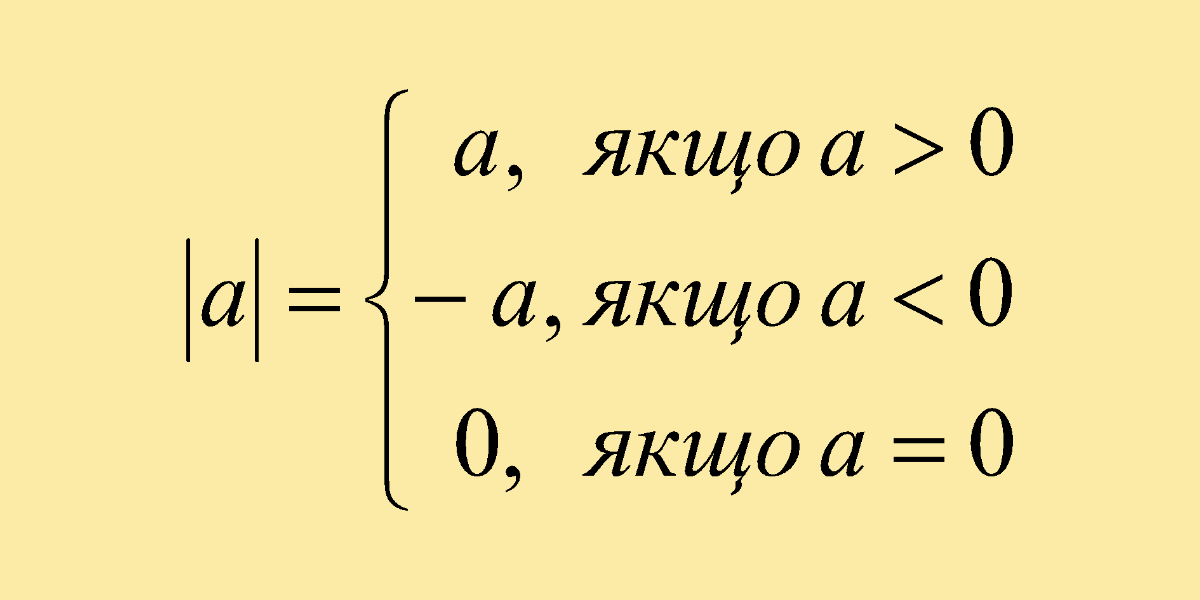














Залишити відповідь