Паралелепіпед просторовий багатогранник, де кожна з шести граней являє собою паралелограм, ніби витягнута коробка з паралельними стінками, що тримаються в ідеальному балансі. Ця фігура виникає скрізь: від цеглин у стіні вашого дому до контейнерів на складі чи навіть піксельних блоків у комп’ютерних іграх. Уявіть, як три пари протилежних граней ковзають паралельно, утворюючи міцну, передбачувану структуру – ось основа його чарівності.
З 8 вершинами, 12 ребрами та 6 гранями паралелепіпед нагадує призму з паралелограмною основою, де бічні ребра паралельні між собою. Об’єм тут дорівнює площі основи, помноженій на висоту, а протилежні грані завжди рівні й паралельні. Така простота ховає глибину: від шкільних задач до моделювання кристалів у науці.
Ця геометрична перлина еволюціонувала від античних ідей до інструменту сучасних технологій, де кожен кут і ребро несе практичний сенс. Далі розберемося, чому паралелепіпед вартий уваги як початківців, так і тих, хто копає глибше.
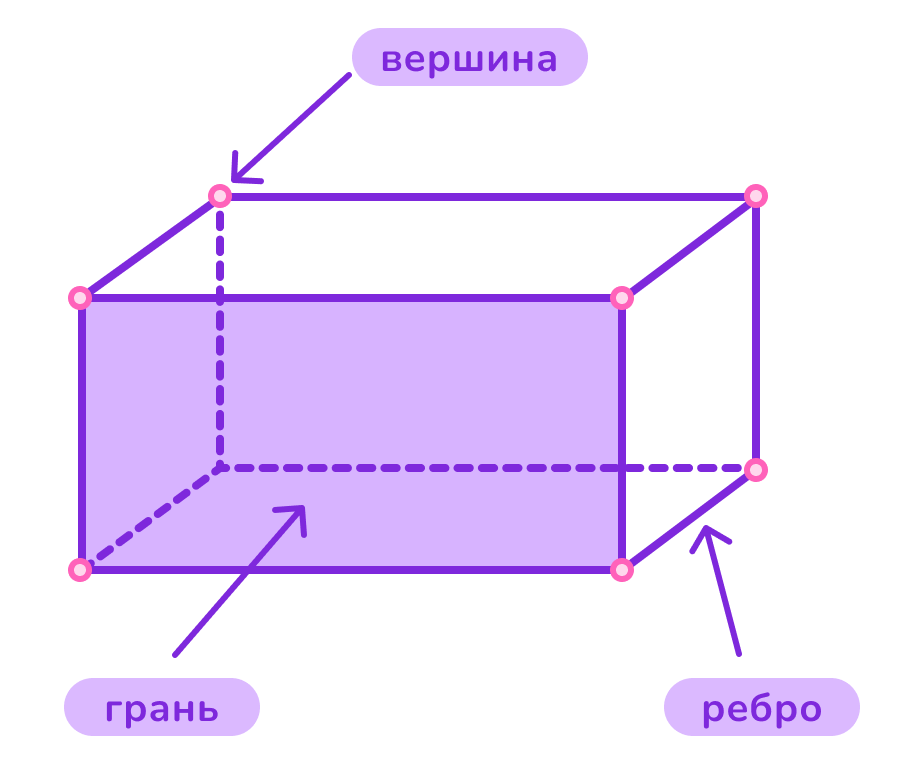
Елементи паралелепіпеда: грані, ребра та вершини в деталях
Серце паралелепіпеда – його елементи, що переплітаються в тривимірну гармонію. Вершини, їх 8, слугують кутами з’єднання, де сходяться по три ребра, утворюючи векторну основу фігури. Ребра, рівно 12, групуються в три пари паралельних: довжини a, b, c задають масштаб, ніби каркас надійного будинку.
Грані – найяскравіша риса: шість паралелограмів, де протилежні пари ідентичні за формою й площею. Суміжні грані ділять спільне ребро, створюючи динамічну мережу. Уявіть, як ця структура тримається на властивості паралельності: жодна грань не “випинається”, все симетрично й стабільно.
Щоб усе запам’яталося, ось ключові характеристики в таблиці. Вона порівнює базові елементи з повсякденними аналогами.
| Елемент | Кількість | Характеристика | Приклад з життя |
|---|---|---|---|
| Вершини | 8 | Точки перетину ребер | Куточки коробки |
| Ребра | 12 | Пари паралельних відрізків | Кромки цегли |
| Грані | 6 | Паралелограми | Стіни кімнати |
Джерела даних: uk.wikipedia.org (станом на 2026 рік). Ця таблиця показує, як абстрактна геометрія оживає в речах навколо. Тепер, коли елементи ясні, перейдімо до різноманіття форм.
Види паралелепіпедів: від простого до витонченого
Паралелепіпеди не одноманітні – їх класифікують за нахилом ребер і формами граней, ніби родина коробок з різними “нахилами”. Загальний паралелепіпед, або похилий, має бічні ребра, не перпендикулярні до основи: грані – довільні паралелограми, ідеал для моделювання скошених структур.
Прямий паралелепіпед вирізняється бічними ребрами, ортогональними до площини основи. Тут чотири бічні грані – прямокутники, основи – паралелограми. Це перехідна форма, близька до реальних ящиків.
- Прямокутний паралелепіпед: всі грані прямокутники, кути прямі – класичний “кімнатний” варіант з трьома розмірами a, b, c.
- Ромбоедр: грані – ромби, ребра рівні в парах, додає симетрії для кристалічних моделей.
- Куб: ідеал, де a = b = c, всі грані квадрати – символ досконалості від грального кубика до атомних ґраток.
Кожен вид розширює можливості: похилий для динамічних форм, прямокутний для будівництва. Обирайте залежно від задачі – від обчислень до візуалізації.
Властивості паралелепіпеда: чому він такий надійний
Властивості роблять паралелепіпед математичним шедевром. Протилежні грані рівні за площею й паралельні – це гарантія стабільності, ніби дзеркальні стіни в лабіринті. Діагоналі, чотири всього, дорівнюють парами, перетинаються в центральній точці й діляться навпіл, створюючи симетричний центр мас.
З будь-якої вершини виходять три ребра, що задають вектори a, b, c; їхня сума з протилежними дорівнює нулю. У координатах вершини легко виразити: від (0,0,0) до (a,b,c) з комбінаціями. Ця векторна природа ідеальна для програмування 3D-моделей.
- Паралельність площин граней: протилежні завжди ||.
- Рівність протилежних ребер у довжині та напрямку.
- Центральна симетрія: фігура обертається на 180° навколо центру без змін.
Такі риси пояснюють, чому паралелепіпед – основа для складніших структур у фізиці та інженерії. А тепер – до серця обчислень.
Формули для паралелепіпеда: об’єм, площа та діагоналі з прикладами
Обчислення – ключ до практичності. Об’єм загального паралелепіпеда V = S_осн × h, де h – відстань між основами. Через вектори: V = |a · (b × c)|, скалярний потрійний добуток, що враховує нахил.
Для прямокутного спрощується: V = a × b × c. Площа поверхні S = 2(S_ab + S_bc + S_ca), де S_ab = a×b×sin(γ) для загального, але для прямокутного S = 2(ab + bc + ca). Діагональ d = √(a² + b² + c²).
Розгляньте задачу: паралелепіпед з a=3, b=4, c=5 (прямокутний). V=60, S=2(12+20+15)=94, d=√50≈7.07. Для похилого з kутом 60° між a,b: S_ab=3×4×sin60°=10.39, і так далі.
| Вид | Об’єм | Площа поверхні | Діагональ |
|---|---|---|---|
| Прямокутний | abc | 2(ab+bc+ca) | √(a²+b²+c²) |
| Загальний | |[a,b,c]| | 2(‖a×b‖ + ‖b×c‖ + ‖c×a‖) | Векторна формула |
| Куб | a³ | 6a² | a√3 |
Джерела: uk.wikipedia.org та mathworld.wolfram.com (2026). Ці формули оживають у задачах: від пакування товарів до розрахунку матеріалів.
Історія паралелепіпеда: від Евкліда до сучасності
Корені сягають античності: Евклід у “Началах” (Книга XI) описував подібні призми, закладаючи аксіоми паралельності. Термін “паралелепіпед” – від грецького “параллос” (паралельний) та “епіпедон” (площина), увійшов у вжиток у XVII-XVIII ст. завдяки Декарту та Лейбніцу.
Леонард Ейлер у 1750-х формалізував властивості, пов’язавши з векторами. У XIX ст. кристалографи, як Гауке, використали для класифікації мінералів. Сьогодні – у CAD-системах і VR, де паралелепіпед базовий примітив.
Ця еволюція показує: від теоретичної абстракції до цифрової реальності, паралелепіпед росте з наукою.
Застосування паралелепіпедів у повсякденності та технологіях
У архітектурі цегла – класичний прямокутний паралелепіпед, що витримує навантаження завдяки паралельним граням. Контейнери на кораблях оптимізують об’єм за формулою V=abc, мінімізуючи порожнечі.
У комп’ютерній графіці bounding box – паралелепіпед, що огортає об’єкти для колізій і рендерингу. Кристалографія вивчає ромбоедри в алмазах чи солях. 3D-друк починає з базових блоків, де похилі форми додають складності.
У фізиці моделює напружені поля, у логістиці – штабелювання. Навіть у медицині – CT-сканування апроксимує органи паралелепіпедами для розрахунків.
Цікаві факти про паралелепіпед
Ви не повірите, але досі шукають “ідеальний кубоїд” – раціональний паралелепіпед з цілими ребрами, площами граней і діагоналями. Комп’ютери перебрали мільярди, але загадка відкрита (uk.wikipedia.org).
Зальцбурзький паралелепіпед – залізний артефакт 1885 р., знайдений у вугіллі, вагою 785 г, з отворами – міг бути інструментом чи артефактом? Дебати тривають.
У 4D-просторі гіперпаралелепіпед задає координатні осі, основа тензорних обчислень у AI.
Куб – єдиний платонічний твердотільник з паралелепіпедів, символ Землі в давнині.
Практичні кейси: як використовувати знання про паралелепіпед
Кейс 1: Розрахунок об’єму кімнати 4×5×3 м – V=60 м³, ідеал для вентиляції. Кейс 2: У грі Minecraft блоки – паралелепіпедам, де об’єм визначає ресурси.
Порада: для нахилених – вимірюйте висоту перпендикулярно. У софті як Blender починайте з куба, трансформуйте в паралелепіпед. Це спрощує дизайн меблів чи прототипів.
Така універсальність робить паралелепіпед незамінним: від школи до NASA-моделей.














Залишити відповідь