Інтеграл перетворює хаос кривих ліній на чіткі числа, ніби збирає краплі дощу в повноводну річку. У серці математичного аналізу це поняття узагальнює суму, дозволяючи рахувати площі під складними кривими чи накопичувати швидкості в шлях. Для початківців: інтеграл від функції f(x) на інтервалі [a, b] — це площа фігури під графіком f(x), обмеженої віссю Ox. А для просунутих — фундаментальний інструмент, що пов’язує диференціали з тотальними змінами в системах від фізики до економіки.
Ця магія народилася з потреби виміряти те, що здається невимірним: довжину гіперболи чи об’єм кулі. Розберемося крок за кроком, чому інтеграл — не просто формула, а ключ до розуміння динаміки світу.
Історія інтеграла: від античних вичерпань до геніального спору
Ще в IV столітті до н.е. Евдокс запропонував метод вичерпання, яким Архімед обчислив площу сегмента параболи — прототип інтеграла. Ці давні греки розбивали фігури на нескінченно тонкі смужки, наближаючись до точної площі. Пройшовши тисячоліття, Йоганн Кеплер у 1615 році використав подібні ідеї для об’ємів вина в бочках, називаючи це “характером кривих”.
Справжній прорив стався в XVII столітті. Ісаак Ньютон, у 1665–1666 роках під час чуми в Кембриджі, розробив “потоки” (fluxions) — протодиференціальне числення для опису руху планет. Незалежно Готфрід Лейбніц у 1675 році ввів символ ∫ (витягнуте S від латинського “summa” — сума) та dx для інфінітесималів. Спір про пріоритет розгорівся в 1711 році: Королівське товариство підтримало Ньютона, але обидва внесли фундаментальний вклад, зафіксований у формулі Ньютона-Лейбніца.
У XIX столітті Бернхард Ріман (1854) строгий визначив інтеграл через границі Рімана-сум, роблячи його стійким до розривів. Сьогодні, за даними uk.wikipedia.org, інтеграл еволюціонував у багатовимірні форми, проникаючи в квантову механіку та штучний інтелект.
Невизначений інтеграл: множина первісних
Невизначений інтеграл ∫f(x) dx — це сімейство всіх функцій F(x), чия похідна дорівнює f(x), з доданою сталою C. Інтуїція проста: якщо похідна “розбиває” функцію на шматки, інтеграл збирає їх назад. Наприклад, ∫x dx = (x²/2) + C, бо похідна x²/2 — саме x.
Перед таблицею базових інтегралів зазначимо: вони — наче готові цеглини для складніших конструкцій. Ось ключові:
- ∫1 dx = x + C — базовий, як нулі в лічильнику.
- ∫x^n dx = (x^{n+1}/(n+1)) + C (n ≠ -1) — узагальнення степенів, відкриття Ньютона.
- ∫e^x dx = e^x + C — єдина функція, рівна своїй похідній.
- ∫sin x dx = -cos x + C — коливання перетворюються в зсуви.
- ∫1/(1+x²) dx = arctan x + C — кут до кола.
Після списку додамо: ці формули перевірені диференціюванням, і з них будуються складніші методи. Для просунутих: невизначений інтеграл — це операція в кільці функцій, де C відображає неоднозначність обернення диференціювання.
Визначений інтеграл: границя до точності
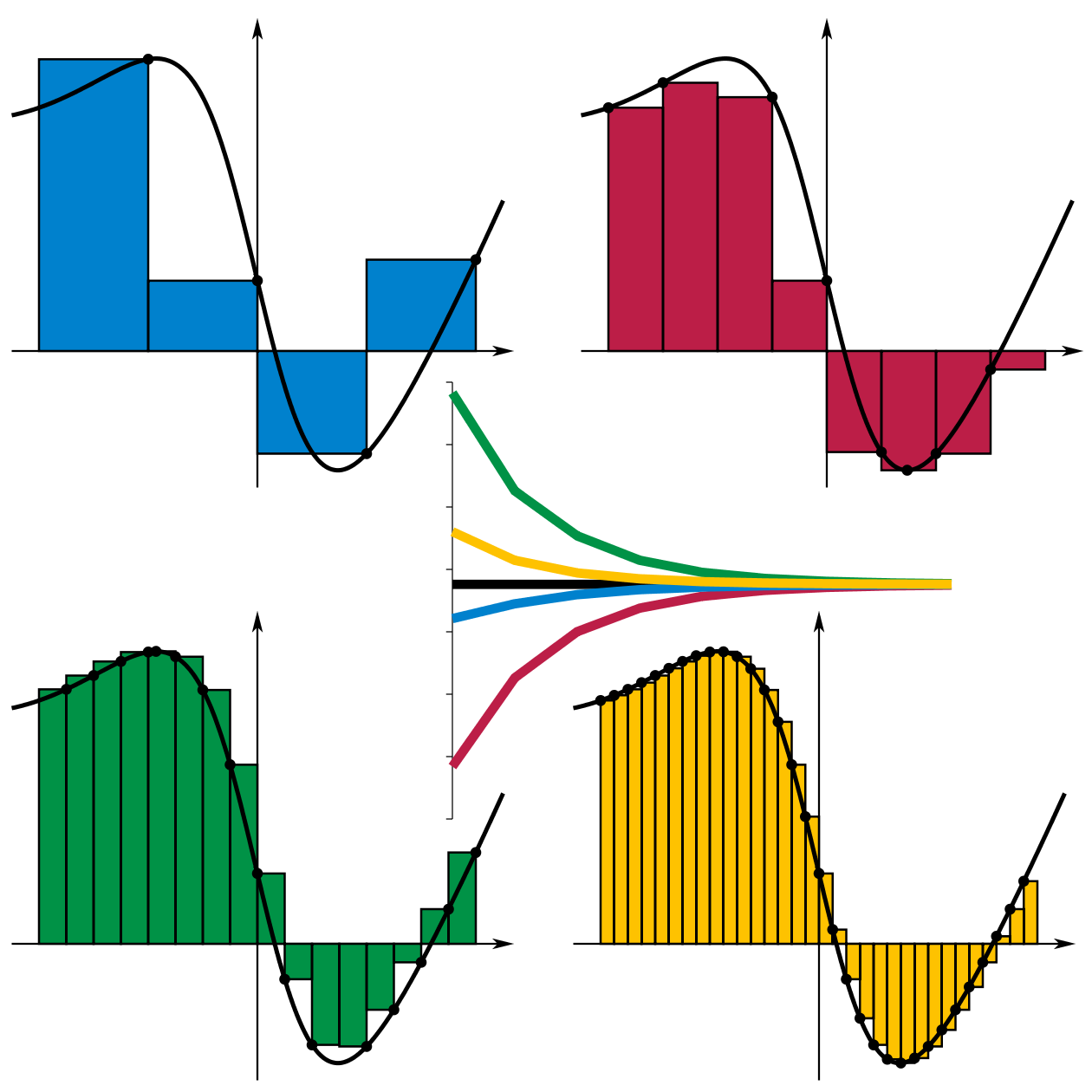
Визначений інтеграл ∫_a^b f(x) dx фіксує число — границю сум f(x_i) Δx при Δx → 0. Ріман у 1854 році ввів це строго: розбиваємо [a,b] на n частин, сумуємо прямокутники, беремо границю. Геометрично: площа під кривою від a до b, з знаками (під віссю — від’ємна).
Властивості захоплюють: лінійність ∫(αf + βg) = α∫f + β∫g, адитивність ∫_a^b = ∫_a^c + ∫_c^b. Середнє значення теореми гарантує: існує c, де f(c) = (1/(b-a)) ∫_a^b f(x) dx.
Геометричний сенс інтеграла: площа, об’єм, довжина
Криволінійна трапеція — класичний образ: тонкі смужки висотою f(x_i), шириною Δx, сума дає площу. Для об’ємів тіл обертання — метод дисків: V = π ∫_a^b [R(x)]² dx, де R(x) — радіус.
Довжина дуги L = ∫_a^b √(1 + (y’)²) dx — для гладких кривих. Уявіть: від параболи до спіралі Фібоначчі, інтеграл вимірює природні форми.
Таблиця порівняння типів інтегралів допоможе розібратися:
| Тип | Визначення | Результат | Приклад |
|---|---|---|---|
| Невизначений | Сімейство первісних | Функція + C | ∫x dx = x²/2 + C |
| Визначений (Рімана) | Границя Рімана-сум | Число | ∫_0^1 x dx = 1/2 |
| Неправильний | Границя на ∞ або розривах | Число або розбіжний | ∫_1^∞ 1/x² dx = 1 |
Джерела даних: Wolfram MathWorld та uk.wikipedia.org. Ця таблиця показує еволюцію від абстрактного до конкретного.
Формула Ньютона-Лейбніца: серце інтегрального числення
Чарівна формула: ∫_a^b f(x) dx = F(b) – F(a), де F — первісна f. Доведена через середню теорему Лагранжа, вона спрощує життя: не треба границь сум! Використовуйте для ∫_0^π sin x dx = [-cos x]_0^π = 2.
Ньютон бачив її в потоках, Лейбніц — в сумах. Сьогодні це міст між диференціалами та тоталами.
Застосування інтегралів: від фізики до сучасних технологій
У фізиці шлях s = ∫ v(t) dt — якщо v(t) = 2t, то s = t² від 0 до 5 с = 25 м. Робота A = ∫ F(x) dx для змінної сили. Центр мас: x̄ = (∫ x dm)/M.
Економіка: чиста теперішня вартість NPV = ∫_0^T c(t) e^{-rt} dt. У графіці: растеризація кривих через інтеграли. Навіть у машинному навчанні 2025–2026 років (тренди з NeurIPS): інтеграли в байєсівських мережах для ймовірностей, Gaussian processes для регресії.
Інженерія: напруження в балках ∫ M(x) dx / EI. Реальні кейси: моделювання траєкторій дронів чи оптимізація сонячних панелей.
Методи обчислення інтегралів: від аналітичних до чисельних
Заміна змінної: ∫ sin(2x) dx, нехай u=2x, du=2 dx → (1/2) ∫ sin u du = – (1/2) cos(2x) + C.
- Виберіть u(g(x)), du = g'(x) dx.
- Перепишіть інтеграл у u.
- Поверніться до x.
Інтегрування частинами: ∫ u dv = uv – ∫ v du, LIATE-правило для вибору. Приклад: ∫ x e^x dx = x e^x – ∫ e^x dx = (x-1)e^x + C.
Для неаналітичних — чисельні: трапеційне правило, Сімпсона. У Python з SciPy.quad() — точність 10^{-15}.
Цікаві факти про інтеграли
Архімед вичерпав параболу за 2000 років до Ньютона. ∫_{-∞}^∞ e^{-x²} dx = √π — Гауссов інтеграл без елементарного доведення. У квантовій механіці амплітуда = ∫ ψ* H ψ dx. Найскладніший: ∫ e^{-x²} dx — функція помилки erf(x), критична для статистики. А в 2026 році нейромережі використовують стохастичні інтеграли для дифузійних моделей генеративного AI.
Інтеграл оживає в кожній симуляції клімату чи фінансовій моделі. Він не статичний — еволюціонує з потреб, від класичної механіки до квантових комп’ютерів, де квантовий інтеграл обчислює неможливе класично.














Залишити відповідь