Пряма лінія на графіку ховає в собі простоту, яка править світом математики та повсякденних розрахунків. Лінійна функція — це математичний інструмент, де залежна змінна y змінюється пропорційно до незалежної x за формулою y = kx + b. Тут k визначає нахил лінії, а b — точку, де пряма перетинає вісь y. Ця формула перетворює хаос чисел на чітку траєкторію, ніби дорога, що веде прямо до мети.
Уявіть прогулянку: кожен крок уперед додає фіксовану відстань. Якщо k дорівнює 2, то за кожен одиничний крок по x ви піднімаєтеся на 2 одиниці по y. А b просто зсуває всю лінію вгору чи вниз. Графік завжди виходить ідеально рівною прямою — жодних вигинів чи сюрпризів. Саме ця передбачуваність робить лінійну функцію королевою початкової алгебри.
Область визначення охоплює всі дійсні числа, бо x може бути будь-яким. Те саме стосується значень y. Тепер розберемося глибше, чому ця функція така потужна і як її використовувати на практиці.
Формула лінійної функції: розбір по елементах
Серце лінійної функції б’ється в рівнянні y = kx + b. Коефіцієнт k, або кутовий коефіцієнт, показує, наскільки швидко змінюється y при зміні x на одиницю. Якщо k позитивне, графік росте праворуч; негативне — падає. Нулеве k перетворює все на горизонтальну лінію y = b, стабільну, як рівень моря.
Вільний член b — це висота старту. При x=0, y=b автоматично. Ця пара k і b повністю описує функцію. Наприклад, у функції y = 3x – 2 лінія стартує з точки (0, -2) і піднімається з нахилом 3. Щоб знайти точку перетину з віссю x (нуль y), розв’яжіть 0 = 3x – 2, отримайте x = 2/3. Прості обчислення, але вони відкривають двері до складніших задач.
Чому саме така форма? Бо це найпростіший поліном першого степеня. Будь-яка пряма на площині записується так, доводить теорія аналітичної геометрії. uk.wikipedia.org підтверджує: це базове поняття елементарної математики.
Графік лінійної функції: чому завжди пряма
Побудова графіка — справа кількох хвилин. Оберіть два значення x, наприклад 0 і 1, обчисліть y і з’єднайте точки прямою. Для y = 2x + 1: при x=0, y=1; при x=1, y=3. Лінія готова. Навіть на калькуляторі чи Excel це виглядає як магія — вхідні дані перетворюються на візуальну модель.
Нахил визначає напрямок: крутий для великого |k|, пологий для малого. Паралельні лінії мають однаковий k, перпендикулярні — добуток k1 * k2 = -1. Ці правила допомагають у геометрії та фізиці, де траєкторії перетинаються під кутом.
- Позитивний k: монотонно зростаюча функція, корисна для прогнозів зростання.
- Негативний k: спадна, ідеальна для втрат чи зменшення.
- k=0: константа, стабільність у моделях.
Після побудови перевірте: чи проходить лінія через обчислені точки? Якщо ні, перерахуйте. Цей метод масштабується на будь-які інтервали, роблячи графіки інструментом аналізу.
Властивості лінійної функції: що робить її унікальною
Лінійна функція монотонна: або завжди росте, або спадає, без поворотів. Максимуми чи мінімуми? Лише на краях інтервалу, якщо обмежити область. Корінь — одна точка, де y=0, за винятком горизонтальної лінії.
Таблиця властивостей полегшує запам’ятовування. Ось порівняння для типових випадків:
| Коефіцієнт k | Знак функції | Нахил графіка | Приклад |
|---|---|---|---|
| Додатний | Зростає | Праворуч вгору | y = 4x + 1 |
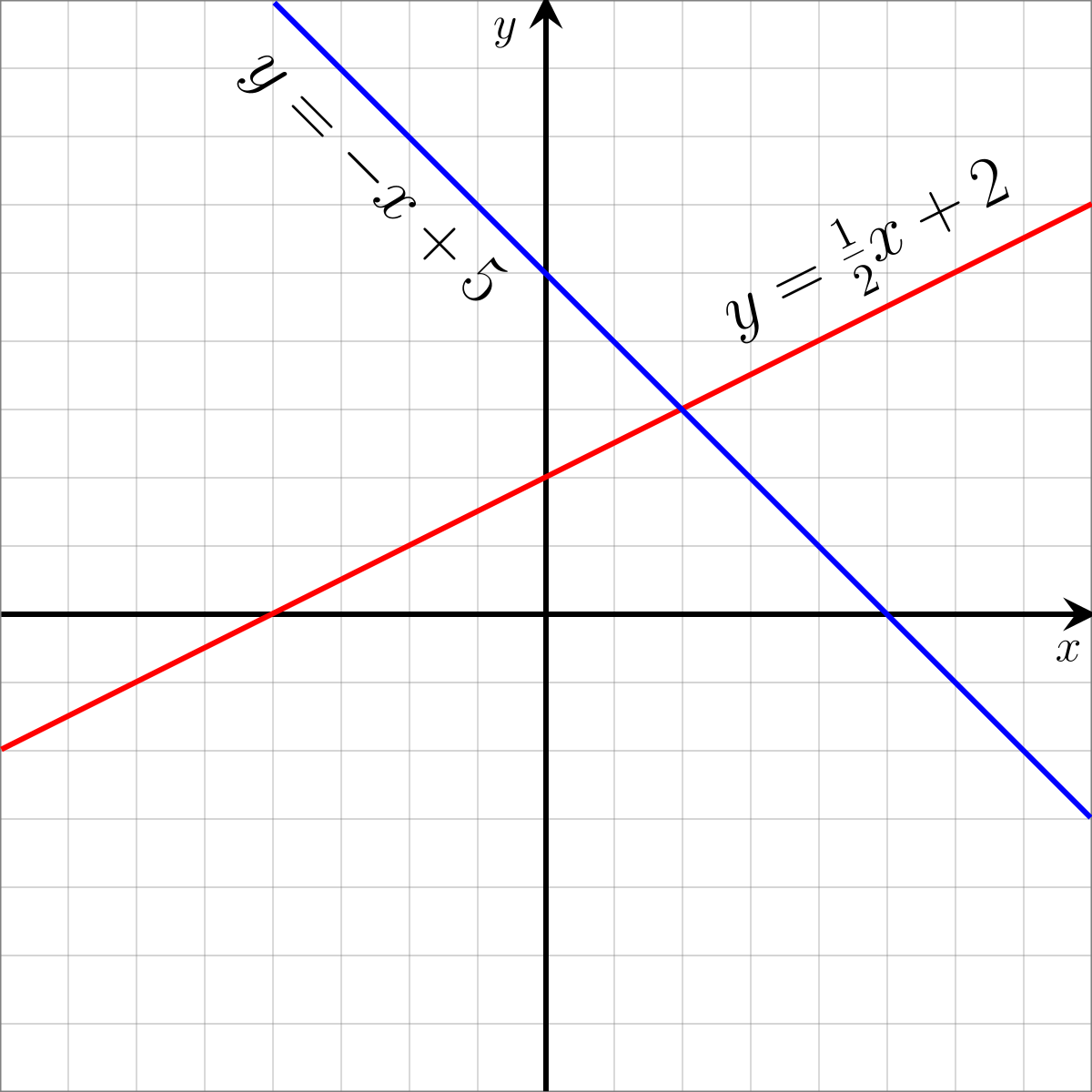
| Від’ємний | Спадна | Праворуч вниз | y = -x + 5 |
| Нуль | Константа | Горизонталь | y = 3 |
Джерела даних: mathab.com.ua. Ця таблиця показує, як k диктує поведінку. Проміжки знаків залежать від кореня: праворуч від нього знак k, ліворуч протилежний.
Унікальність у лінійності: зміна x на Δx дає зміну y рівно kΔx. Це основа для апроксимацій складніших кривих.
Побудова графіка крок за кроком
Спочатку складіть таблицю значень. Візьміть y = -0.5x + 4 для x від -2 до 4:
- Оберіть x: -2, -1, 0, 1, 2, 3, 4.
- Обчисліть y: для x=-2, y=5; x=0, y=4; x=4, y=2.
- Позначте точки: (-2,5), (0,4), (4,2).
- З’єднайте прямою.
Результат — спадна лінія. У GeoGebra чи Desmos це автоматизується, але ручний розрахунок тренує інтуїцію. Для обмеженого інтервалу, скажімо x ∈ [0,5], графік — відрізок.
Застосування лінійної функції в реальному житті
У повсякденні лінійні функції всюди. Автомобіль мчить рівномірно: відстань s = v t, де v — постійна швидкість (k=v), початкова s=0 (b=0). За годину при 60 км/год — 60 км. Просте, але рятує в логістиці.
Економіка: ціна товару p = c q + f, де q — кількість, c — ціна за одиницю, f — фіксовані витрати. Магазин продає яблука по 10 грн/кг + доставка 50 грн. Для 5 кг: 100 грн. Попит чи пропозиція часто моделюють так.
Фізика: температура за законом Ньютона охолоджується лінійно на коротких інтервалах. У програмуванні — лінійна інтерполяція для графіки в іграх чи анімації.
Сучасніше: лінійна регресія в data science. Аналізуйте продажі: y = 20x + 100, де x — реклама в тисячах грн. Прогнозуйте з точністю 90% для лінійних трендів. У 2025-2026 роках машинне навчання починає з лінійних моделей, бо вони швидкі та інтерпретовані.
Порівняння з іншими функціями: лінійна проти кривих
Квадратична y = x² вигинається параболою — росте нелінійно, як траєкторія м’яча. Експоненційна y = 2^x вибухає, ідеальна для відсотків чи вірусів. Лінійна ж — стабільна апроксимація для малих змін.
Коли використовувати? Лінійна для постійних швидкостей, квадратична — для прискорень. Перехід від лінійної до складніших розширює горизонти моделювання.
Практичні кейси: лінійні функції в дії
Кейс 1: Фітнес. Втрата ваги w = -0.5 d + 80, де d — дні тренувань. За 10 днів: 75 кг. Мотивує реалістичними прогнозами.
Кейс 2: Бюджет. Витрати e = 15 h + 200, h — години роботи. Плануйте фінанси точно.
Кейс 3: Програмування. У Python: def linear(x): return 3*x -1. Графік у matplotlib — миттєвий аналіз даних.
Ці приклади показують, як теорія оживає в Excel чи коді, роблячи математику інструментом успіху.
Типові помилки та як їх уникнути
Початківці часто плутають k з b: k — зміна, b — старт. Помилка в графіку: забувають точку (0,b). Розв’язок: завжди перевіряйте x=0.
Інша пастка — думати, що всі прямі лінійні. Так, але в обмеженому домені кусково-лінійні складніші. Тренуйтеся на таблицях, щоб інтуїція виростала.
Лінійні функції — місток до алгебри, де простота породжує силу. Експериментуйте з графіками, моделюйте своє життя — і математика заграє новими фарбами.














Залишити відповідь