Трикутник ховає в собі таємниці простоти й складності водночас, ніби гострий клинок, що розтинає площину на рівні частини. Його площа – ключ до розуміння геометрії, від шкільних задач до реальних проєктів у будівництві дахів чи комп’ютерній графіці. Почнемо з основи, яка працює для будь-якого трикутника, незалежно від форми чи розмірів.
Базова формула площі: половина основи на висоту
Найпростіший рецепт: візьміть довжину основи, помножте на висоту, опущену до цієї основи, і поділіть на два. Формула виглядає так: S = (1/2) × a × h, де a – основа, h – висота. Чому саме половина? Бо два таких трикутники складаються в паралелограм, а його площа – повний добуток основи на висоту. Уявіть, як два гострих трикутники зчіплюються краями, утворюючи прямокутну форму – ось і весь секрет.
Приклад з життя: уявіть дах будинку у формі трикутника з основою 10 метрів і висотою 4 метри. Площа покрівлі: S = (1/2) × 10 × 4 = 20 квадратних метрів. Додайте черепицю чи металочерепицю – і отримаєте точний розрахунок матеріалів. А якщо висоти немає? Тоді переходьте до хитріших методів, бо геометрія не терпить прогалин.
Ця формула універсальна, але вимагає точного вимірювання висоти. У гострокутних трикутниках вона падає всередину, у тупокутних – зовні. Перевіряйте напрямок, щоб уникнути мінусових значень у розрахунках.
Формула Герона: коли відомі тільки сторони
Герон Александрійський, винахідник парової турбіни ще в I столітті, подарував нам магію для “безвисотних” трикутників. Спочатку обчисліть півпериметр p = (a + b + c)/2, де a, b, c – сторони. Потім S = √[p(p – a)(p – b)(p – c)]. Ця формула – як детектив: з трьох підозрюваних (сторін) вичисляєш таємницю площі.
Розберімо приклад. Трикутник з сторонами 5, 5 і 6 см. Півпериметр p = (5+5+6)/2 = 8. S = √[8(8-5)(8-5)(8-6)] = √[8×3×3×2] = √144 = 12 см². Ідеально для рівнобедреного! Джерело таких формул – класична геометрія, зафіксована в uk.wikipedia.org.
Чому вона працює? З тригонометрії: sin γ = висота / сторона, а за теоремою косинусів виводиться вираз під коренем. Не турбуйтеся про доведення зараз – головне, що це рятує землемірів у поле, де висоту не виміряєш рулеткою.
Площа прямокутного трикутника: катети як союзники
Прямокутний трикутник – улюбленець інженерів, бо один кут 90°, і катети a, b самі стають основою та висотою. S = (1/2) × a × b. Просто, як два помножити й наполовину! Гіпотенуза c за Піфагором c = √(a² + b²), але для площі вона не потрібна.
Приклад: катети 3 і 4 см, гіпотенуза 5. S = (1/2)×3×4 = 6 см². Це класичний 3-4-5 трикутник, основа багатьох конструкцій – від сходів до рам. У будівництві такий розрахунок визначає об’єм бетону для фундаментів.
Гумор у тому, що забути про “половину” – типова пастка. Отримаєте площу прямокутника замість трикутника, і дах “злетить” удвічі дорожче.
Особливі трикутники: рівносторонній і рівнобедрений
Рівносторонній – досконалий, всі сторони a, кути 60°. Висота h = (√3/2) × a, тому S = (√3/4) × a². Для a=10 см: S ≈ (1.732/4)×100 ≈ 43.3 см². √3 – магічне число, що робить його стійким у архітектурі, як у пірамідах.
Рівнобедрений: дві сторони рівні, висота ділить основу навпіл. Знайти h = √(b² – (a/2)²), де b – рівні сторони, a – основа. Потім S = (1/2)×a×h. Приклад: b=5, a=6, h=√(25-9)=4, S=12 см² – той самий, що в Герона.
Ці форми всюди: логотипи, дахи, навіть у природі – листя багатьох рослин.
Тригонометрія в дії: дві сторони та кут
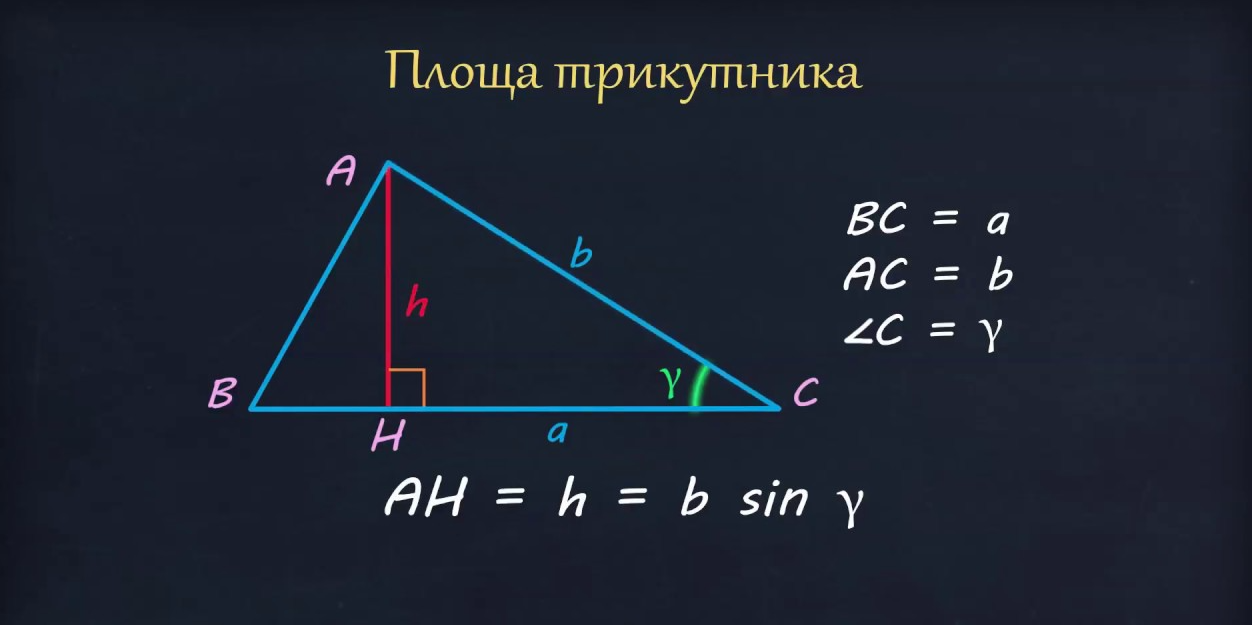
Коли відомі сторони a, b і кут γ між ними, S = (1/2) × a × b × sin(γ). Синус – ключ, бо висота = b × sin(γ). Для γ=90° sin=1, виходить прямокутний випадок.
Приклад: a=5, b=7, γ=60°, sin60°=√3/2≈0.866. S=(1/2)×5×7×0.866≈15.2 см². Корисно в навігації чи 3D-моделюванні, де кути вимірюють теодолітами.
Пам’ятайте: sin(180°-γ)=sin(γ), тож тупі кути не лякають.
Типові помилки при розрахунку площі трикутника
- Забули поділити на 2: отримаєте паралелограм замість трикутника – класика новачків.
- Неправильна висота: у тупокутному трикутнику висота зовні, інакше площа “зникне”.
- Плутанина з півпериметром у Герона: p – не периметр, а половина!
- Ігнор одиниць: см і м не помножиш без конверсії.
- Калькулятор без перевірки: sin у радіанах? Перемкніть на градуси.
Уникайте цих пасток – і ваші розрахунки стануть бездоганними. Перевіряйте завжди: площа має бути додатною!
Площа за координатами вершин: для цифрової ери
У світі GPS і графіки вершини A(x1,y1), B(x2,y2), C(x3,y3). Формула: S = (1/2) | x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2) |. Це половина детермінанта матриці координат.
Приклад: A(0,0), B(4,0), C(0,3). S=(1/2)|0(0-3)+4(3-0)+0(0-0)|= (1/2)×12=6. Ідеально для програмування ігор чи карт.
У 3D: проєктуйте на площини xy, yz, zx і візьміть √(Sxy² + Syz² + Szx²)/2. Корисно для CAD-програм.
| Метод | Відомі дані | Формула | Приклад застосування |
|---|---|---|---|
| Базова | Основа, висота | S = (1/2)ah | Дах будинку |
| Герона | Три сторони | S = √[p(p-a)(p-b)(p-c)] | Землемірство |
| Прямокутний | Катети | S = (1/2)ab | Фундамент |
| Тригонометр. | Дві сторони, кут | S = (1/2)absinC | Навігація |
| Координати | Вершини (x,y) | (1/2)|det| | Комп. графіка |
Таблиця базується на стандартних формулах з uk.wikipedia.org. Порівняйте – обирайте за даними.
Ще більше способів: радіуси кіл і медіани
З радіусом вписаного кола r: S = r × p, де p – півпериметр. Для описаного R: S = (a b c)/(4R). Рівняння зв’язують коло з трикутником – краса евклідової геометрії.
Через медіани ma, mb, mc: S = (4/3) √[σ(σ-ma)(σ-mb)(σ-mc)], σ=(ma+mb+mc)/2. Рідко, але корисно в аналітичній геометрії.
У 1885 році математик Бренан зібрав понад 100 формул – від простих до екзотичних. Сьогодні комп’ютери беруть на себе, але розуміння основ робить вас майстром. Експериментуйте з прикладами, і трикутники відкриють вам секрети світу.
Застосовуйте в житті: від садового газону до дизайну татуювань. Геометрія жива, і площа – її серцебиття.














Залишити відповідь