Коло манить своєю досконалою симетрією, ніби втіленням космічної гармонії, де кожна точка на межі рівновіддалена від центру. Радіус — це той невидимий промінь, що тримає все разом, відстань від серця фігури до її краю. Без нього не обчислити ні довжину колеса велосипеда, ні орбіту планети. Розберемося, як його вирахувати в будь-якій ситуації, від шкільних задач до реальних проєктів.
Радіус як основа геометрії кола
Уявіть центр кола — точку O, звідки до будь-якої точки на окружності, скажімо A чи B, відстань завжди однакова. Ця відстань і є радіусом r. Він визначає все: від площі до довжини обрізу. Діаметр d просто удвічі більший — d = 2r, як міст через річку, що з’єднує протилежні береги. У шкільних підручниках це базове правило, але в житті воно рятує інженерів від промахів.
Число π, приблизно 3,14159, — незмінний супутник усіх формул. Воно народилося з спостережень за колом тисячі років тому, коли вавилоняни наближали його до 3. Сьогодні комп’ютери вираховують мільярди його цифр, але для нас вистачить кількох знаків.
Найпростіший розрахунок: радіус за діаметром
Діаметр виміряти легше — це пряма лінія через центр. Щоб знайти радіус, просто ділимо навпіл. Формула r = d / 2 гранично проста. Візьмімо колесо велосипеда з діаметром 70 см. Радіус вийде 35 см — половина, і крапка.
- Вимірюйте діаметр рулеткою чи штангенциркулем.
- Ділите на 2.
- Готово! Точність залежить від інструменту.
Цей метод ідеальний для майстрів: чи то заміна шин, чи креслення. Пам’ятайте, помилка в міліметрі множиться на оберти — і велосипед хитнеться.
Радіус через довжину окружності
Окружність — це “периметр” кола, довжина C. Формула C = 2πr перевертається на r = C / (2π). Якщо знаєте обхват, діліть на подвоєне π. Приклад: мотузка навколо бочки довжиною 125,6 см. r = 125,6 / (2 × 3,14) ≈ 20 см. Легко, правда?
Уявіть гонщика на треку: довжина 400 м, радіус повороту розраховується так само. Точне π з калькулятора — 3,1415926535 — дає мінімальну похибку. За даними Khan Academy, це стандарт для шкільних задач.
Знаходимо радіус за площею кола
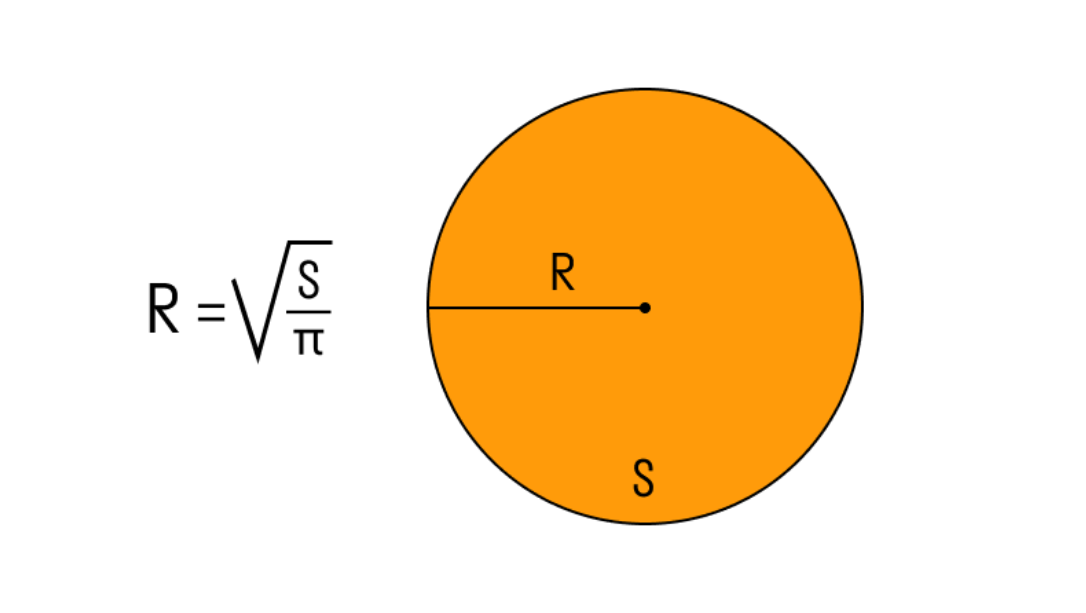
Площа S = πr² ховає радіус під коренем. Щоб витягти, r = √(S / π). Квадратна площа? Ділите на π, берете корінь. Блін на сковорідці займає 78,5 см². r = √(78,5 / 3,14) ≈ 5 см — ідеальний розмір!
- Обчислюйте S точно.
- Ділите на π.
- Корінь квадратний — і радіус готовий.
Цей спосіб хитрий для дизайнерів: скільки тканини на круглу скатертину? Плюс, у програмуванні для графіки — базовий інструмент.
| Величина | Формула для радіуса r | Приклад (r ≈ ?) |
|---|---|---|
| Діаметр d | r = d / 2 | d=10 см → r=5 см |
| Довжина C | r = C / (2π) | C=31,4 см → r=5 см |
| Площа S | r = √(S / π) | S=78,5 см² → r=5 см |
Таблиця базується на стандартних формулах з uk.wikipedia.org. Порівняйте — всі сходяться на r=5 см. Зручно для перевірки!
Просунуті методи для досвідчених
Не тільки базові формули. У координатній площині рівняння кола (x – h)² + (y – k)² = r² ховає радіус під коренем з правої частини. Центр у (3,4), r²=25 — r=5. Простий спосіб для програмування чи креслень CAD.
Хорда довжиною l на відстані d від центру: r = √( (l/2)² + d² ) — теорема Піфагора в дії. Для сектора з кутом α і площею — теж формули. У 3D радіус сфери R визначає об’єм 4/3 πR³, але принцип той самий.
Ви не повірите, але в астрономії радіус орбіти Землі — 149 млн км, вирахуваний за паралаксом. Глибоко, але логічно.
Радіус кола в реальному житті: від колеса до космосу
Коло — скрізь. Радіус колеса авто впливає на кліренс і швидкість: r=30 см — стандарт для седана. У спорті: баскетбольний м’яч r≈12 см, для точних кидків. Архітектори рахують радіус куполів соборів — як у Флоренції, де Брунеллескі використав геометрію.
У медицині — МРТ сканує з радіусом поля зору. Смартфони малюють інтерфейси круглими іконками з точним r. Навіть у кулінарії: піца діаметром 30 см, r=15 см — порція на двох. Практично, корисно, захопливо!
Типові помилки при знаходженні радіуса кола
Багато плутають коло з кругом: коло — межа, круг — фігура всередині. Не діліть C на π, а не 2π — помилка удвічі! Забувають корінь при площі — r² лишається. У координатах плутають центр з радіусом.
- Використовуйте π=3,14 для точності, не 22/7 всюди.
- Перевіряйте одиниці: см чи м?
- Калькулятор — друг, але розумійте формулу.
Уникайте — і ваші розрахунки стануть бездоганними. Найчастіша пастка: плутанина довжини з площею.
Історія та цікавинки числа π і радіуса
Архімед у III ст. до н.е. наблизив π до 22/7, обводячи коло багатокутниками — геніально! Сьогодні знаємо 100 трлн цифр. Радіус Землі — 6371 км, за яким моделюють клімат. У грі Fortnite кола зменшуються з точним r — гравці в захваті.
Гумор: чому коло не йде на дієту? Бо π незмінне! Серйозно ж: у GPS радіус сигналу — ключ до позиції. Розрахунки радіуса — місток від античності до супутників.
Експериментуйте: намалюйте коло, виміряйте — і відчуйте магію. А якщо задача складніша, комбінуйте формули. Далі — тільки практика!














Залишити відповідь